达西定律

达西定律专题

渗透率

渗透率是与电或热的传导性相似的一种性质。

油藏岩石具有让流体在联通孔隙孔隙中流动的能力，这种能力成为渗透率。

岩石的渗透率取决于有效孔隙度，因此渗透率受岩石颗粒大小、形状、粒径分布（分选）、颗粒充填方式以及固结和胶结程度等因素影响。砂岩颗粒间黏土或胶结物的类型也影响渗透率，蒙皂石和高岭石遇淡水膨胀，会堵塞孔隙。

当低速流占优势时，渗透率的倒数代表孔隙介质对流体流动产生的粘滞阻力。习惯上把符合这种条件的流动成为”粘性流“，或正式成为”斯托克斯流（stocks）“

渗透率的分类

原始渗透率(基质渗透率)

沉积物沉积和成岩过程中形成的。

次生渗透率

压实、胶结、破碎和溶解作用过程中由于岩石骨架的变化而形成的。

绝对渗透率

如果岩石百分百饱和一种流体（单相流），如油、气、水，为绝对渗透率。

有效渗透率

岩石饱和一种以上流体，则其渗透率被称为有效渗透率。

油的有效渗透率：$$$ K_o $$$;
气的有效渗透率：$$$ K_g $$$;
水的有效渗透率：$$$ K_w $$$。

相对渗透率

当岩石中存在一种以上的流体时，任一相的有效渗透率与绝对渗透率之比为该相流体的相对渗透率（$$$ K_r $$$）。油、气水的相对渗透率分别是：

$$K_{ro} = K_o / k$$ $$K_{rg} = K_g / k$$ $$K_{rw} = K_w / k$$

渗透率大小的影响因素

渗透率低于1mD的储层就被认为是致密储层，

（1）砂岩颗粒的形状和大小；
（2）层理；
（3）胶结作用；
（4）破碎和溶解作用。

单位

渗透率的常用单位是D，相当于黏度为1$$$ mPa·s $$$的流体在$$$ 1atm/cm $$$的压力梯度驱动下，以$$$ 1{cm^3}/s $$$的速率在单位截面为1$$$ m^2 $$$的样品中的流动。

$$Q({cm^3} / s) = \frac{ K(D) × A({cm^2}) }{ μ(mPa·s) } \frac{ \Delta p(atm)}{L (cm) }$$

由于达西单位比较大，一般使用毫达西(mD)表示渗透率更为方便，在SI单位制中，D表示为${μm}^2$。

$$1D = 0.986923 × 10^{-12} {m}^2 = 0.986923 × 10^{-8} {cm}^2 = 0.986923 {μm}^2$$

达西定律

1856年，发过水力工程师Henry Darcy在研究净化用的砂滤器中水的流动时提出的流体渗流方程，已成为石油工程师计算渗透率标准公式之一。

达西定律表明单位横截面积渗透性介质的体积流速（即体积流量）与势能梯度成正比，与流体的黏度成反比。该比例系数就是渗透率。

适用条件

• 渗流流体为单相牛顿流体，服从牛顿内摩擦定律，应力与应变呈线性关系；
• 多孔介质性质稳定。渗流过程中孔隙结构保持不变，反应多孔介质渗流能力的渗透率值为一常数；
• 多孔介质性质和流体性质分别为渗流方程中的独立参数。多孔介质和渗流流体之间的相互作用对流体流动的影响很小，可以忽略；
• 多孔介质中流体以层状态流动；
• 达西定律适用于黏性流，即流体的流速足够低，且与压力梯度城正比。
• 流体不予多孔介质发生化学反应。

达西定律可以罗占到除水之外其他流体；
达西定律中的比例系数实际上就是流度：$K/μ$；
在地球重力场中，达西定律与流动方向无关。

简单微分形式

$$v = \frac{q}{A_c} = - \frac{K}{μ} \frac{dp}{dL}$$

$$ v $$ —— 流体流速，$$ cm/s $$；
$$ q $$ —— 流量，$$ cm^3/s $$；
$$ K $$ —— 孔隙岩石的渗透率，D；
$$ A_c $$ —— 岩心样品的截面积，$$ {cm}^2 $$；
$$ μ $$ —— 流体黏度，$$ mPa·s $$；
$$ L $$ —— 岩石样品的长度，$$ cm $$；
$$ \frac{dp}{dL} $$ —— 渗流方向上的压力梯度，$$ atm/cm $$。

上式无需考虑流体密度和流体黏度的影响。

推导方程

$$ q = \frac{{A_c}K}{μ} \frac{dp}{dx} $$

$$ K = \frac{qμL}{({p_1}-{p_2}) {A_c}} $$

$$ {p_1} $$，入口压力，atm；
$$ {p_2} $$，出口压力，atm；

绝对渗透率实验

岩石的固有属性，在单向流体流过岩石时测得的。

液体法绝对渗透率

恒温和给定压力梯度条件下，测量一确定体积的液体流过岩心所需的时间。

$ K = \frac{μ V L}{A \Delta pt} $

$$ K $$ —— 绝对渗透率，D；
$$ μ $$ —— 在观测温度下的流体黏度，$$ mPa·s $$；
$$ V $$ —— 流体体积，$$ {cm}^3 $$；
$$ L $$ —— 岩石长度，$$ cm $$；
$$ A $$ —— 岩心横截面积，$$ {cm}^2 $$；
$$ \Delta p $$ —— 压差，$$ Pa，p_1 - p_2 $$；
$$ t $$——一定体积液体流过岩心所需要的时间，s。

气体法绝对渗透率

当气体的平均自由程大于孔隙直径时，气体分子的随机运动会使气体分子穿过孔隙或从孔隙壁上滑过。

考虑到气体的膨胀效应，使用平均流量和平均压力来计算渗透率。

$$ Q_1 $$ —— 气体进口流量，$$ {cm}^3/s $$；
$$ Q_2 $$ —— 气体出口流量，$$ {cm}^3/s $$；

由于气体膨胀的原因，$Q_1 < Q_2$，应用等温条件下爱的理想气体定律：

$ p_1 Q_1 = p_2 Q_2 = p_{av} Q_{av} $
$ p_{av} = \frac{p_1+p_2}{2} $
$ Q_{av} = \frac{p_2 Q_2}{p_{av}} $

记录在出口段流过一定体积气体的时间和两端的压力$$$ p1 $$$、$$$ p_2 $$$ 平均流量 $$$ Q{av} $$$ 等于气体体积除以该时间。求解渗透率的达西方程为：

$$K(D) = \frac{Q_{av} μ L}{A (p_2 - p_1)}$$

Forchheimer惯性阻力

达西定律具有局限性，仅限于低速体积流量。

在油藏中，特别是远离生产井和注入井的地方，体积流量一般非常低，因此可以应用达西定律。
但在具有高压力梯度的高流量近井地区可能引起不可忽视的惯性效应，称为速敏表皮效应。这种
效应在产气井井眼附近和射孔井段特别普遍，在这些地带，低粘度的气体能产生很高的流量。

气体滑脱效应(Klinkenberg效应)

气体渗透率>绝对渗透率

产生差异的原因主要是由于气体滑脱效应或克林肯伯格(Klinkenberg)效应和上覆压力的影响。

测量渗透率值与$$ \frac{1}{p_m} $$$的交会图延长到$ 1/p_m = 0 $(即$ p_m $$无限大)。这时候得到渗透率近似等于液体渗透率$$$ K_L $$$。

孔隙渗透率$$$ K_a $$$与液体渗透率的关系为：

$ K_a = c \frac{1}{p_m} + K_L $

$$ p_m $$ —— 测量压力，为$$ (p_1 + p_2) / 2 $$；
$$ c $$ —— 直线斜率；
$$ K_L $$ —— 等效流体渗透率，即绝对渗透率K。

$ c = b K_L $

$$ b $$ —— 孔隙几何因子，依赖于孔隙张开尺寸，并与毛管半径成反比。

围压对渗透率的影响

多孔介质的渗透率对介质受到的净压缩应力的大小及其受力过程敏感。岩样夹持器围压的增
加，岩石的渗透率降低。

相对渗透率实验

岩石化学和物理性质的函数，对岩石和流体的温度以及润湿性都比较敏感。

目前测定两相相对渗透率（汽油、气水、水油）的方法已经得到了很好的发展。

$$K_{rg} = \frac{k_{eg}}{K}$$ $$K_{rw} = \frac{k_{ew}}{K}$$ $$K_{ro} = \frac{k_{eo}}{K}$$

$$ K $$ —— 绝对渗透率；
$$ K_{eg},K_{er},K_{eo} $$ —— 分别是气、水、油在一定饱和条件下的有效渗透率；
$$ K_{rg},K_{rr},K_{ro} $$ —— 分别是气、水、油在一定饱和条件下的相对渗透率；

稳态法

使两种流体以稳定的流量流入和流出岩心。

实验方法

测量油和水的相对渗透率，将已饱和水或油的岩心放入岩心夹持器中，在液体进口端安装压力传感器。如果使用回压调节器使孔隙内保持高压，则应在岩心的出口端再安装一个压力传感器，这样可以测量驱替压差。使用恒速泵提供稳定的水或油量，在混合室内混好后注入岩心的端面。每种流体的流速可以通过调节泵速控制。

以一定的速率注入水和油，监测出口端水和油的流量，当出口水和油的流量与入口相等时，就达到了稳态。此时，岩心内水和油的饱和度为常数。

记录流量和压差。取出岩心，称重。根据岩心质量、孔隙体积和两相流体的密度计算饱和度。由下式可计算不同饱和度下的有效渗透率。
然后把岩心重新放入夹持器，调整流量改变岩心内的饱和度。重复以上步骤，直至得到足够的数据建立渗透率与饱和度之间的函数关系。
对于水——油系统：

$$K_{ew} = \frac{Q_w μ_w L}{A \Delta p_0} = \mathcal{f} (S_w)$$ $$K_{eo} = \frac{Q_o μ_o L}{A \Delta p_0} = \mathcal{f} (S_w)$$

假设两相毛管压力可以忽略，且$$$ pw = p_o $$$，则特定饱和度下的$$$K{rw} $$$和$$$ K_{ro} $$$有下式子得出。$$$ S_w $$$可由一下关系计算：

$$M = (D_M) + S_w V_p \rho + (1-S_w)V_pp_0$$ $$S_w = \frac{M - D_M - V_p \rho_o}{V_p(\rho_w - \rho_o)}$$

$$ D_M $$ —— 干燥岩心的质量，g；
$$ V_p $$ —— 岩心的孔隙体积，mL；
$$ M $$ —— 岩心和内部流体的总质量，g；
$$ \rho $$ —— 密度，g/{cm}^3；

计算公式

$$ K_a = \frac{ 2 P_a · Q_0 · μ · L × 10^2 }{ A · (p_1^2 - p_2^2) } $$

$$ P_a $$ —— 大气压力，$$ MPa $$；
$$ Q_0 $$ —— 绝对大气压时，空气流量，$$ {cm}^3/s $$；
$$ μ $$ —— 气体黏度，$$ mpa·s $$；
$$ L $$ —— 岩心长度，$$ cm $$；
$$ A $$ —— 岩心横截面积，$$ {cm}^2 $$；
$$ p_1 $$ —— 测岩样渗透率时的进口压力，$$ Mpa $$；
$$ p_2 $$ —— 测岩样渗透率时的出口压力，$$ Mpa $$；

非稳态法测量

用水或气驱替岩心中的流体。所有方法基于均质岩心的假设，可以忽略毛管压力和重力。

实验方法

交替法

基于相对渗透率与平均流体饱和度的函数。只需要达西定律并且只建立相对渗透率和岩心平均饱和度的函数关系图，而不需要岩心末端口的饱和度，所以交替法比较简单。

JBN(Johnson bossler Naumann)法

基于岩心相对渗透率和流体驱替过程中入口端（末端）饱和度的函数关系，要求驱替注入速率是恒定的。此实验过程必须以较高的流速进行以避免毛管末端效应（岩心末端出现异常高的湿相饱和度）。

陶斯（Toth）法

比以上两种方法更为常用。因为它使用与恒速和恒压注入驱替。次方法可由驱替数据直接计算相对渗透滤，因此比其他两种方法有更高的精度。

相对渗透率测量设备及步骤

（1）使岩心100%饱水，用油驱水至不再出水为止（$$$ S{wi} $$$）。用离心机分离驱替出的油水，计量被油驱出的水量，计算初始含水饱和度。
（2）静置岩心12小时，使其达到毛管平衡。
（3）对于恒速注入，调节定量泵，使驱替液以恒定流速进入岩心。对于恒压注入，调整气驱柱塞泵以恒定压力输送驱替液。
（4）开启驱替泵，并计时。
（5）若使用水和原油驱替系统，用带刻度的离心集液管计量出口的液体并计时；若使用气液驱替系统，用气体流量计计量出口的气体，用带刻度的量筒计量出口的液体并计时。
（6）当出口躯体液中不再含油时或达到预定注入水体积后，停止实验（本实验为3倍孔隙体积）。
（7）如果使用原油，用离心机分离油和水，记录每一段时间驱除的油水量及时间。
（8）计算累计油水量，以注入孔隙体积倍数为横坐标绘制累积出油曲线。
（9）对没一时段计算油水的流率、相对渗透率和平均含水饱和度$$$ S{w(av)} $$$。

$$S_{w(av)} = S_{wi} + \frac{V_{oil(produced)}}{V_p}$$

低渗非达西流

特征曲线

非线性段

在低压力梯度范围内，渗流曲线呈非线性。随压力梯度的增大，渗流量增大。渗流量与压力梯度呈指数关系，指数大于1。

$$Q=a_1 (grad P)^n$$

拟线性段

较高压力梯度下，渗流曲线呈拟线性。拟线性段的反向延长线不通过坐标原点，而与压力梯度轴有一正相交点。

拟线性段渗流量和压力梯度的关系：$Q=a_2(gradP)-b$

临界面压力梯度

由非线性段过渡到拟线性段的点成为临界点C。

临界点所对应的压力梯度为临界压力梯度$gradP_c$。

渗透率越低临界压力梯度越大，非达西渗流特征约显著。

拟启动压力梯度

在非线性段上任一一点作切线，切线都会与压力梯度轴有一正值交点，成为拟启动压力梯度$gradP_b$

在非线性段随压力梯度的增大，拟启动压力梯度增大。

在拟线性段拟启动压力梯度为定值。

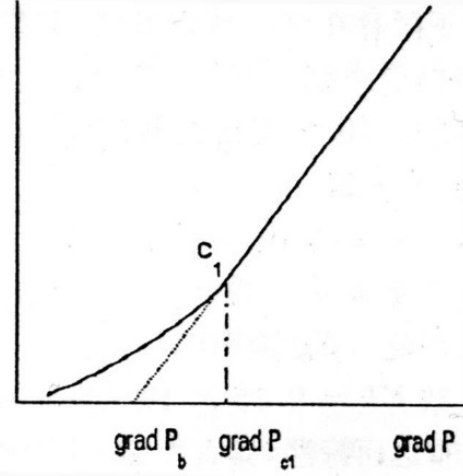
非达西渗流情况

• 非牛顿流体渗流
• 非层流流态渗流
• 变形多孔介质渗流
• 非等温渗流
• 低渗多孔介质渗流

非达西流渗流条件

• 低渗多孔介质孔隙喉道细小，流体与孔隙介质之间的作用力对流体的影响已不能忽略。
• 细小孔隙喉道，油气是细小喉道存在明显的启动压力梯度。
• 使渗流规律不具备达西渗流所使用的渗流条件，呈现低渗非达西渗流特征。

低渗非达西渗流机理

启动压力梯度

• 固液界面存在分子作用力，成吸附滞留层。
• 吸附滞留层的厚度约为0.1μm。
• 低渗多孔介质孔隙吼道更细小，孔径和吸附滞留层厚度在同一数量级，甚至更小。
• 细小孔隙中，吸附滞留层对流体流动的影响不可忽略，存在启动压力梯度。

流动孔隙数

• 储层中的孔隙系统是由无数孔径大小不等的孔隙组成。
• 孔径越小，启动压力越大。
• 在非线性段，随压力梯度的增大，参与流动的孔隙数增多。
• 达到临界压力梯度以后，流动孔隙数成为定值。

附加渗流阻力

• 拟启动压力梯度反应附加渗流阻力。
• 在非线性段，岁流动孔隙数增多附加渗流阻力增大。
• 在拟线性段，附加渗流阻力位定值。
• 不管是非线性段还是拟线性段，附加渗流阻力的影响都存在。

低渗非达西渗流的综合判据

渗流状态的影响因素

1. 从中高达西渗流到低渗非达西渗流是个渐变过程。
2. 两种渗流状态的判别标准并非是渗透率的单值函数。
3. 它取决与多孔介质孔隙结构参数和流体性质参数：
   3.1：孔隙结构参数：孔隙半径、喉道半径、孔吼比、配位数、孔隙迂回度、孔隙分布密度等。
   3.2：流体性质参数：流体黏度和密度。

低渗非达西渗流的判别依据

低渗非达西渗流特征判别依据

• 拟启动压力梯度。拟启动压力梯度为0，即达西线性渗透；拟启动压力梯度>0，即为低渗非达西渗流。

影响拟启动压力梯度的物理量

渗透率K、孔隙半径R、吼道半径r、流体粘度μ、流体密度ρ

低渗非达西渗流的判别式

$${\lambda}_N = \frac{μ^2}{Kρ} \frac{R}{r}$$ $${\lambda}_N $$ 的单位为Pa，称为压力数 压力数<2，启动压力梯度趋近于0，呈现达西渗流特征； 压力数>5，启动压力梯度影响不可忽略，呈现非达西渗流特征； 2<压力数<5，视为过渡区。 ## 低渗非达西渗流的视渗透率 ### 渗透率的变化 非线性段，随压力梯度的增大，流动孔隙数增多，附加渗流阻力增大。但流动孔隙数增多起主导作用，渗透率呈上升趋势。 在拟线性段，流动孔隙数和附加渗流阻力都为定值。但随压力梯度的增大，附加渗流阻力的影响相对减小，渗透率仍呈上升趋势。 非线性段和拟线性段，随压力梯度的增大渗透率变化规律不同。 ### 视渗透率 如果仍以渗流量和压力梯度的关系来定义储层渗透率的话，则可用下式计算视渗透率： $$ K_s = \frac{Q μ}{A gradP}$$

此式与达西公式的不同点在于，适用于中高渗透性储层的达西公式中，渗透率是定值。而在地神非达西流的情况下，渗透量和压力梯度关系式中的视渗透率是个变量，它随压力梯度的增大而增大。

视渗透率曲线

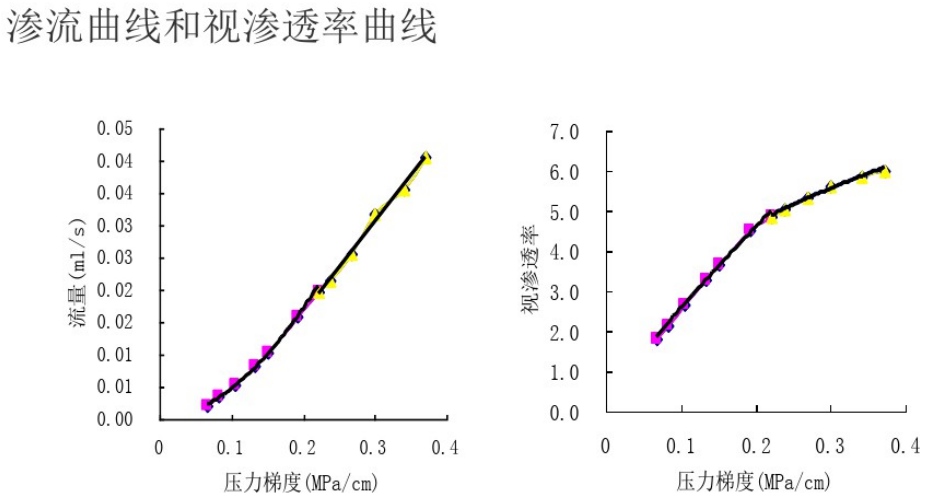
视渗透率定义

启动压力梯度，流动孔隙数，附加渗流阻力都和压力梯度有关，又都影响储层的渗流能力。压力梯度的大小不仅直接影响渗流量的大小，而且影响储层的渗透率。因此，在低渗透储层中压力梯度不同，渗透率也不同，渗透率是压力梯度的函数。

所以，把低渗透储层中，随压力梯度的变化所引起的渗透率变化，成为低渗透储层的视渗透率。

视渗透率变化特征

• 视渗透率远比气测渗透率低。
• 视渗透率是变量，与压力梯度直接有关。压力梯度月底，视渗透率越低。
• 大于临界压力梯度的情况下，视渗透率明显较高。
• 小于临界压力梯度时，视渗透率明显较低。