实用Python程序设计MOOC-第四章函数和递归

[TOC]

实用Python程序设计MOOC-第四章函数和递归

函数的概念和用法

为什么需要函数？

写了一段平方根的代码，程序里面无数地方都要求平方根，难道需要的地方都把这段代码拷贝一遍?

数百个程序员如何合写一个程序?都在一个. py文件上操作吗?不同程序员实现不同功能，一个程序员要使用另一个程序员写的功能时怎么办?

“函数”：将实现了某一功能，并需要在程序中多处使用的代码包装起来形成一个功能模块(即写成一个”函数”)，那么当程序中需要使用该项功能时，只需写一条语句，调用实现该功能的”函数”即可。

不同的程序员可以分别写不同的函数，拼起来形成一个大程序。

函数的定义

def 函数名(参数1, 参数2....):
	语句体(函数体)

def 函数名():
	语句体(即"函数体")

函数调用和return语句

调用函数：

函数名(参数1, 参数2, ...)

对函数的调用，也是一个表达式。函数调用表达式的值，由函数内部的return语句决定。return语句语法如下:

return 返回值

return语句的功能是结束函数的执行，并将”返回值”作为结果返回。”返回值”是常量、变量或复杂的表达式均可。如果函数不需要返回值，return语句就直接写:

return

return语句作为函数的出口，可以在函数中多次出现。多个return语句的”返回值”可以不同。在哪个return语句结束函数的执行，函数的返回值就和哪个return语句里面的”返回值”相等。

函数使用实例1 : Max函数

def Max(x,y):	#传入形参
	if x > y:
		return X
	else:
		return y
#函数到此结束

n = Max(4, 6)	#传入实参
print(n, Max(20, n)
print(Max("about", "take"))

6 20
take

函数使用实例2 :判断是否是素数的函数

def IsPrime(n):
	if n <= 1 or n % 2 == 0 and n != 2:
		return False
	elif n == 2:
		return True
	else :
		for i in range(3, n, 2):
			if n % i == 0:
				return False
			if i * i > n:
				break
	return True
for i in range(100):
	if(IsPrime(i)):
		print(i, end = " ")

2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97

不返回值的函数

def DrawCircle(x, y, r):
	#下面的代码在屏幕上以(x,y)点为圆心，r为半径画圆
	return	#没有也可以

调用：

DrawCircle(0, 0, 1)

函数返回多个值

def sumAndDifference(x, y):
	return x+y, x-y
s, d = sumAndDifference(10, 5)
print(s, d)

=>155

函数中的变量

• 一个函数内部定义(赋值)的变量，在这个函数外部不能使用
• 不同函数中的同名变量不会互相影响
• 函数中的变量和全局变量(在函数外面定义的变量)同名的情况(假设都叫x)：
  1)如果没有对x赋值，函数中的x就是全局的x
  2)如果对x赋值，且没有特别声明，则在函数中全局的x不起作用，函数中的x就是只在函数内部起作用的x
  3)函数内部可以用global x声明函数里的x就是全局变量x

x = 4	#全局的x 
def f0():
	print("x in f0:", x) #这个x是全局的x
def f1():
	x = 8	#这个x是局部的x，不会改变全局的x
	print("x in f1:", x)
def f2():
	global x	#说明本函数中的x都是全局的x
	print("x in f2:", x)
	x = 5
	print("x in f2:", x)
def f3():
	print("x in f3=", x)	#会出错。因后面有赋值而被当作局部的x，此处没赋值就先使用了，不行
	x = 9

f0() #>> x in f0:4
f1() #>> x in f1:8
print(x) #>>4
f2()
#>> x in f2:4
#>> x in f2:5
print(x) #>> 5
f3() #调用f3会出错

python内置函数

int(x)
float(x)
str(x)
ord(x)
chr(x)
abs(x)
len(x) 
	len("123") 
	len([2,3,4])
max(x)
	x是列表，如max([2,3,5])
min(x)
	x是列表，如min([2,3,5])
max(x1, x2, x3...)
min(x1, x2, x3...)
print(max(1, 2, 3))	#>> 3
print(min("ab", "cd", "af"))	#>>	ab

什么是递归

• 一个概念的定义中用到了这个概念本身，这就叫递归

用递归的方式定义”n的阶乘”

1) “1的阶乘”是1
2）”n的阶乘”就是n乘以”(n-1)的阶乘”

第二句中用到了阶乘这个需要定义的概念

• 一个函数，自己调用自己，就是递归。
• 和调用别的函数无本质区别，可以看作是调用另一个同名同功能函数

def Factorial(n):	#函数返回n的阶乘
	if n < 2:
		return 1 #终止条件
	else:
		return n * Factorial(n - 1)

print(Factorial(4))	#>>24
print(Factoria1(5))	#>>120 

• 递归函数需要有终止条件，否则就会无穷递归导致程序无法终止甚至崩溃
• 递归定义也需要有终止条件，否则无法让人明表。例如”n的阶乘”的定义中的：
  1) “1的阶乘”是1

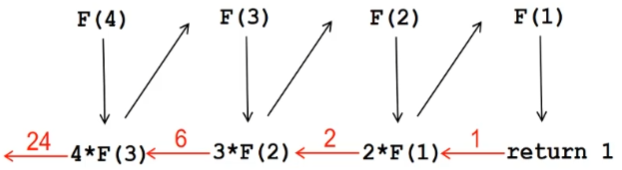
• 求斐波那契数列第n项的函数

def Fib(n):
	if n == 1 or n == 2:
		return 1
	else:
		return Fib(n-1) + Fib(n-2)

def f(n,m):
	if	n== 0:
		return m
	elif m == 0:
		return n
	else:
		if n >= m:
			return f(m, n-m) + 1
		else:
			return f(n, m-n) + 2
print(f(3,4))	#>> 7

递归例题:上台阶

上台阶问题：有n级台阶，每步可以走一级或两级，问有多少种不同的走法？

先做一步，剩下问题和原问题形式相同，规模变小

def ways(n):
	if n == 1:
		return 1
	elif n == 2:
		return 2
	else:
		return ways(n-1) + ways(n-2)	#第一步走一级的走法+第一步走2两级的走法
print(ways(4))	#>> 5

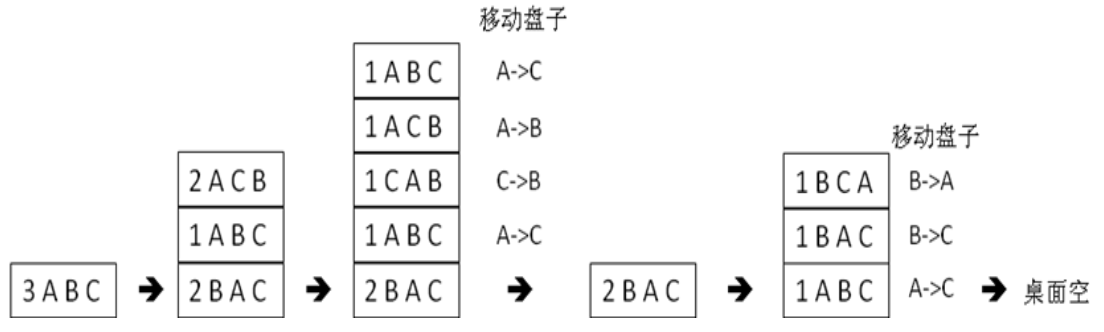
递归例题:汉诺塔(Hanoi)

def Hanoi(n, src, mid, dest):	#将src座上的n个盘子,以mid座为中转,移动到dest座
	if(n == 1):	#只需移动一个盘子
		#直接将盘子从src移动到dest即可
		print(src + "->" + dest)
		return #递归终止
	Hanoi(n-1, src, dest, mid)	#先将n-1个盘子从src移动到mid
	print(src + "->" + dest) #再将一个盘子从src移动到dest
	Hanoi(n-1, mid, src, dest) #最后将n-1个盘子从mid移动到d
n = int(input())
Hanoi(n, 'A', 'B', 'C')

3
A->C
A->B
C->B
A->C
B->A
B->C
A->C

n个盘子需要2^n-1次

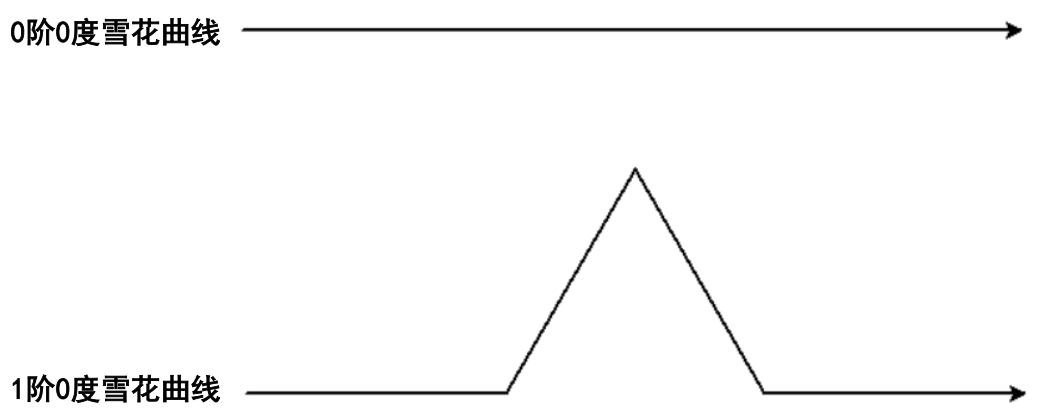
递归例题:绘制雪花曲线(科赫曲线)

雪花曲线的递归定义
1)长为size，方向为x(x是角度)的0阶雪花曲线，是方向x上一根长为size的线段
2)长为size，方向为x的n阶雪花曲线，由以下四部分依次拼接组成：
1.长为size/3，方向为x的n-1阶雪花曲线
2.长为size/3，方向为x+60的n-1阶雪花曲线
3.长为size/3，方向为x-60的n-1阶雪花曲线
4.长为size/3，方向为x的n-1阶雪花曲线

size是整体长度

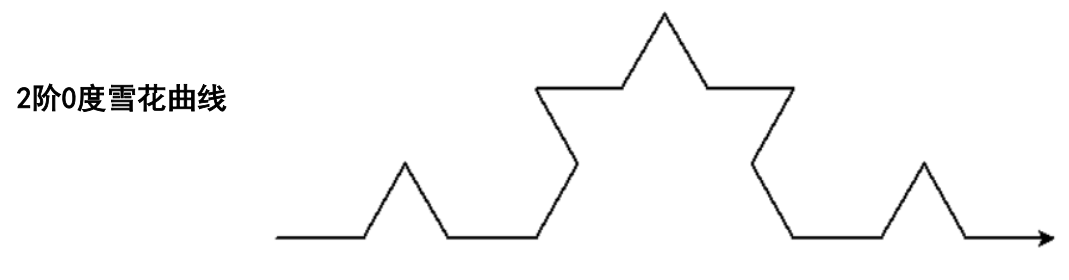
四段一阶的雪花曲线构成
1.长度为size/3，方向为0°的1阶雪花曲线
2.长度为size/3，方向为60°的1阶雪花曲线
3.长度为size/3，方向为-60°的1阶雪花曲线
4.长度为size/3，方向为0°的1阶雪花曲线

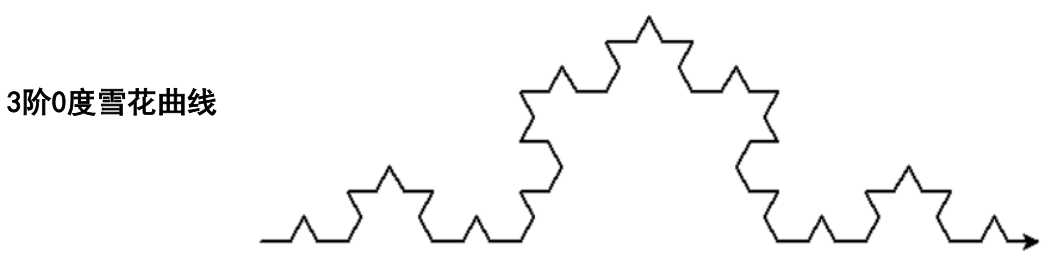
四段二阶的雪花曲线构成
1.长度为size/3，方向为0°的2阶雪花曲线
2.长度为size/3，方向为60°的2阶雪花曲线
3.长度为size/3，方向为-60°的2阶雪花曲线
4.长度为size/3，方向为0°的2阶雪花曲线

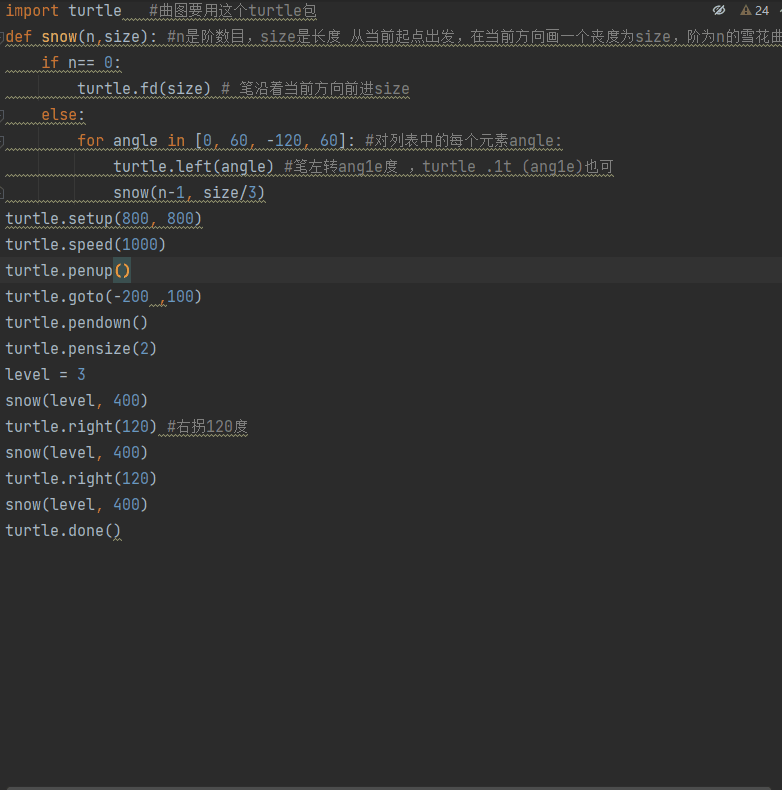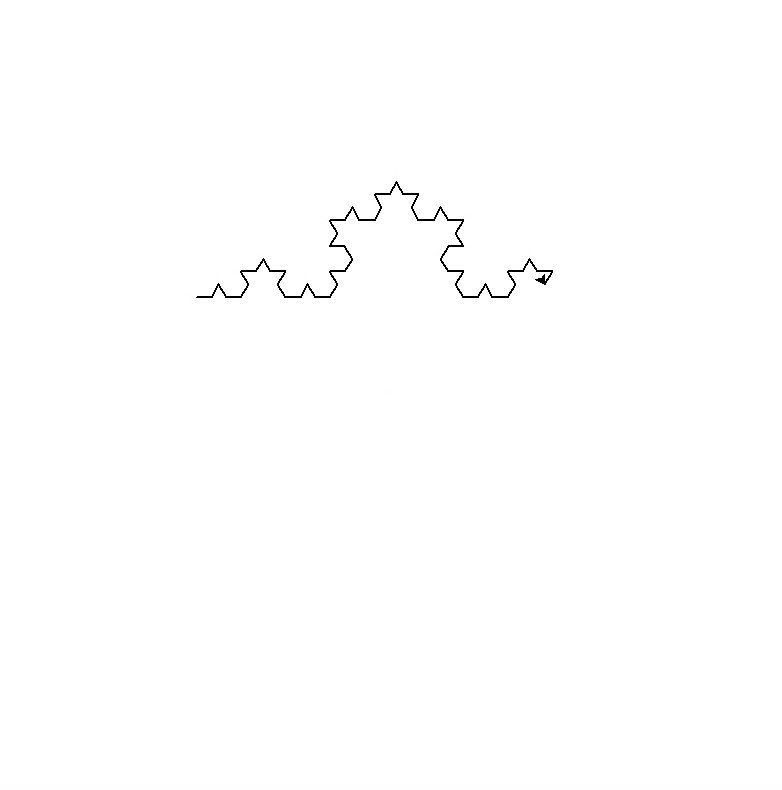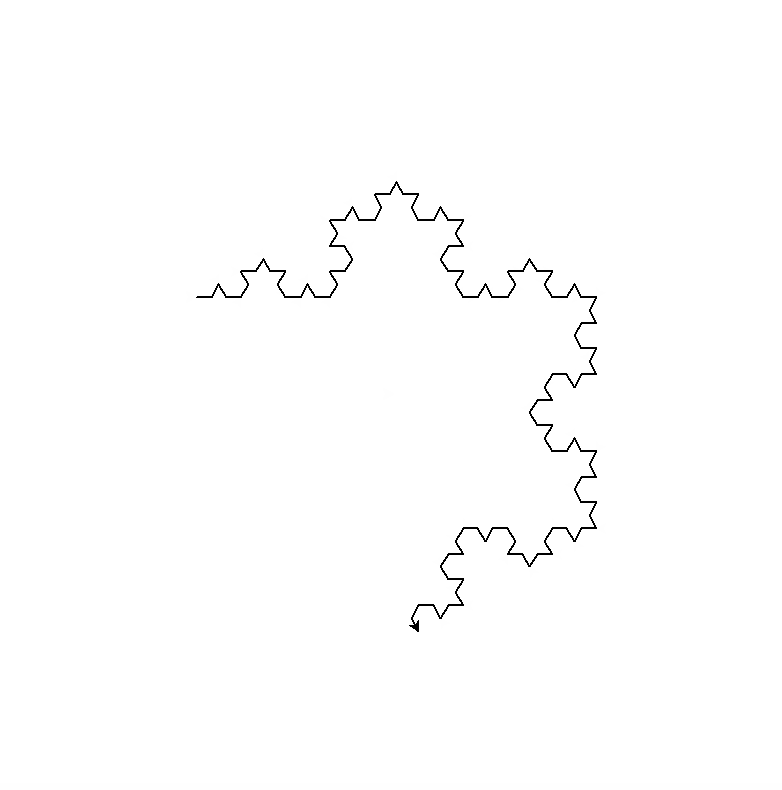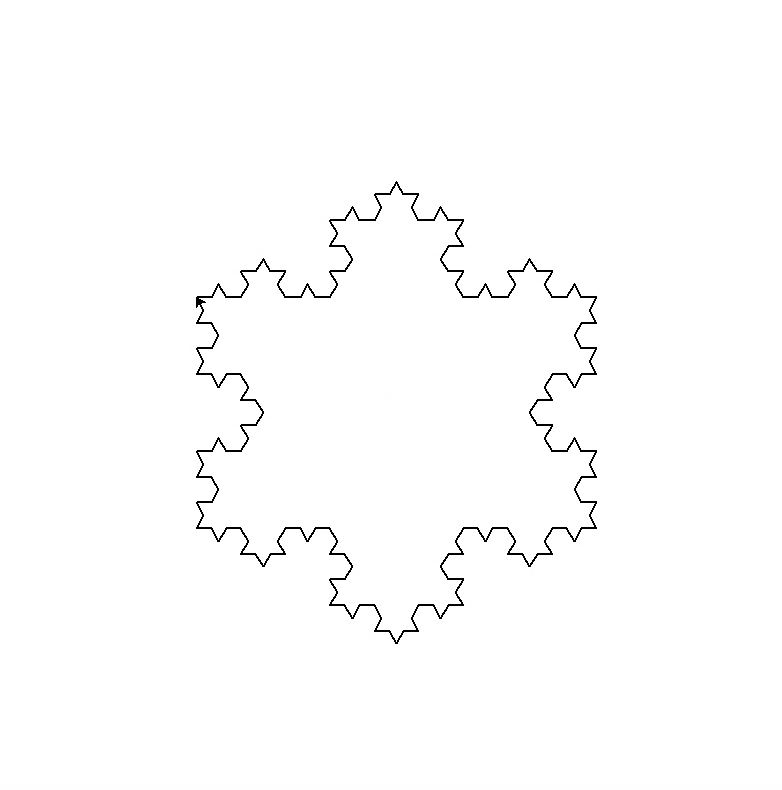
import turtle	#曲图要用这个turtle包
def snow(n,size): #n是阶数目，size是长度 从当前起点出发，在当前方向画一个丧度为size，阶为n的雪花曲线
	if n== 0:
		turtle.fd(size) # 笔沿着当前方向前进size
	else:
		for angle in [0, 60, -120, 60]: #对列表中的每个元素angle:
			turtle.left(angle) #笔左转ang1e度 ，turtle .1t (ang1e)也可
			snow(n-1, size/3)

turtle.setup(800, 600)#窗口缺省位于屏幕正中间，宽高800*600像素，窗口中央坐标(0,0)
#初始笔的前进方向是0度。正东方是0度，正北是90度
turtle.penup() #抬起笔
turtle.goto(-300, -50) #将笔移动到-300, -50位置
turtle.pendown() #放下笔
turtle.pensize(3) #笔的粗度是3
snow(3, 600)	#绘制长度为600 ,阶为3的雪花曲线，方向水平
turtle.done()	#保持绘图窗口

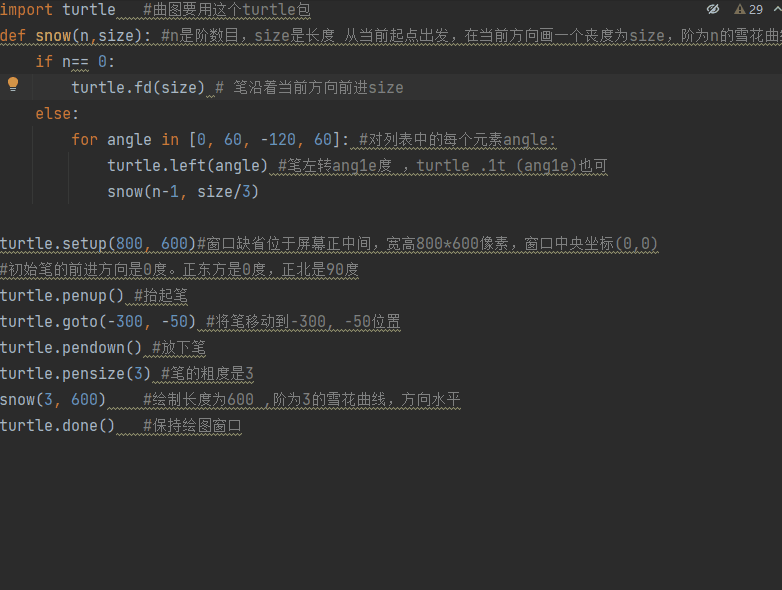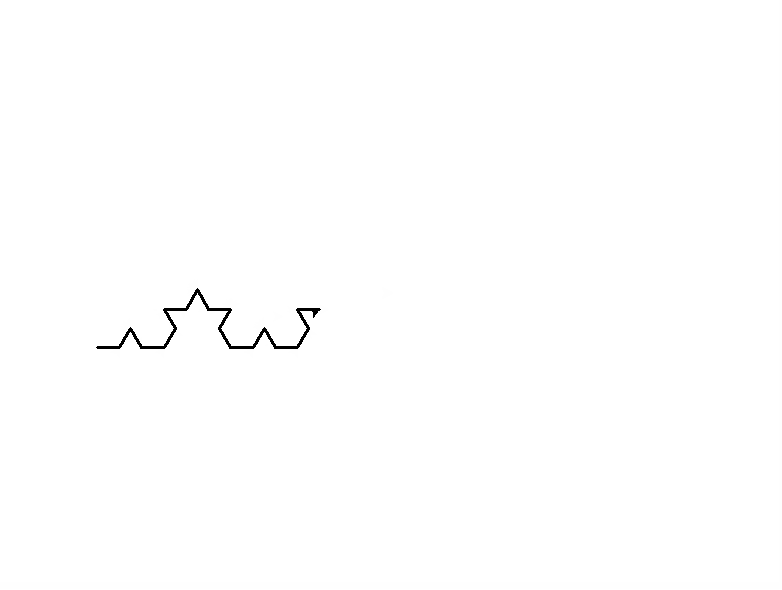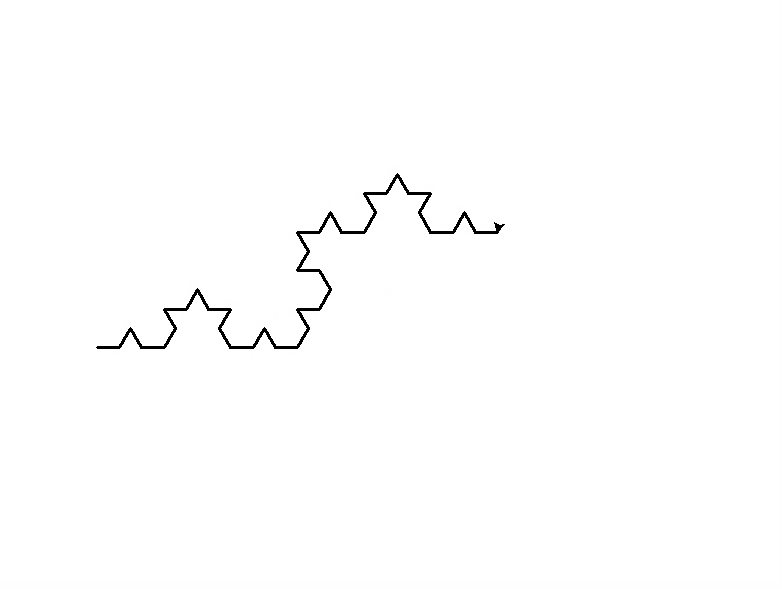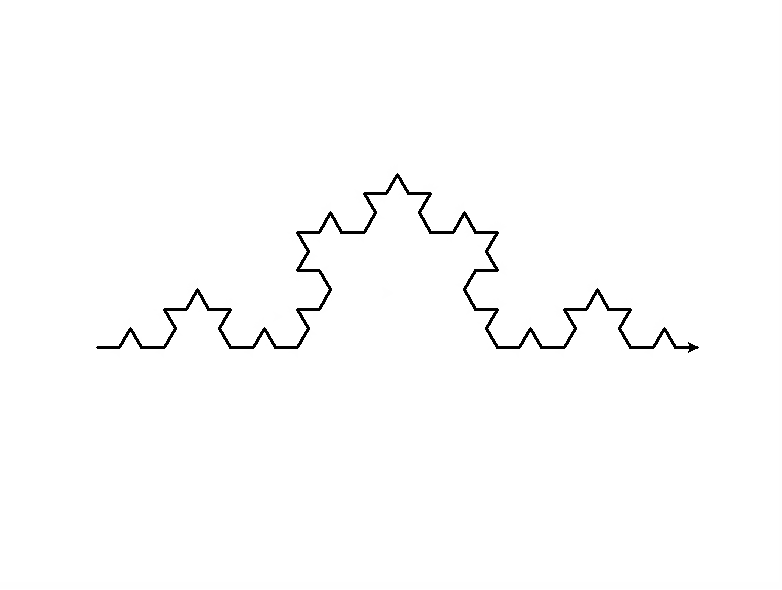
窗口正中心位置是(0, 0)
画图要有画笔，画笔需要有方向
雪花曲线画完之后笔的方向和初始方向一样

• 画整个雪花

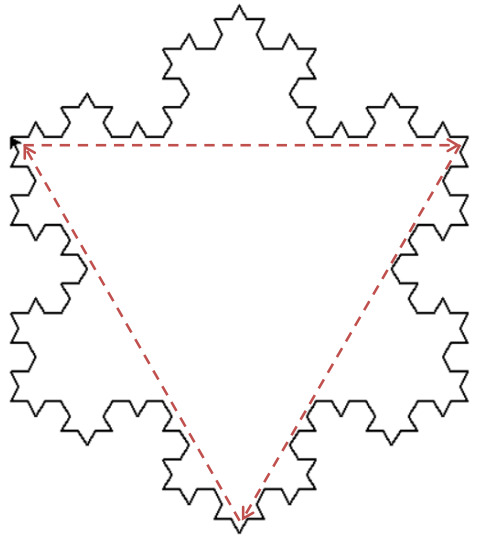
turtle.setup(800, 800)
turtle.speed(1000)
turtle.penup() 
turtle.goto(-200, 100)
turtle.pendown()
turtle.pensize(2)
level = 3
snow(level, 400)
turtle.right(120) #右拐120度
snow(level, 400)
turtle.right(120)
snow(level, 400)
turtle.done()

• 递归问题解法

1.先做一步，观察剩下问题是否和原问题相同，规模更小
2.将一个大问题分解成若干个子问题，有些子问题和原问题都是形式相同，规模更小的
3.选取合适的边界条件

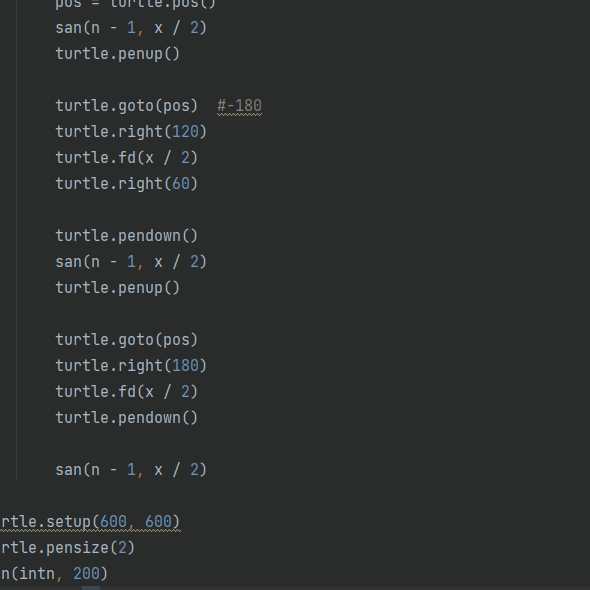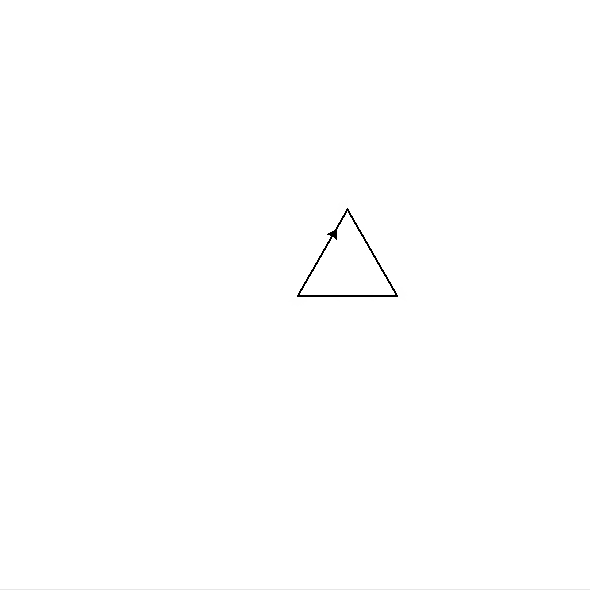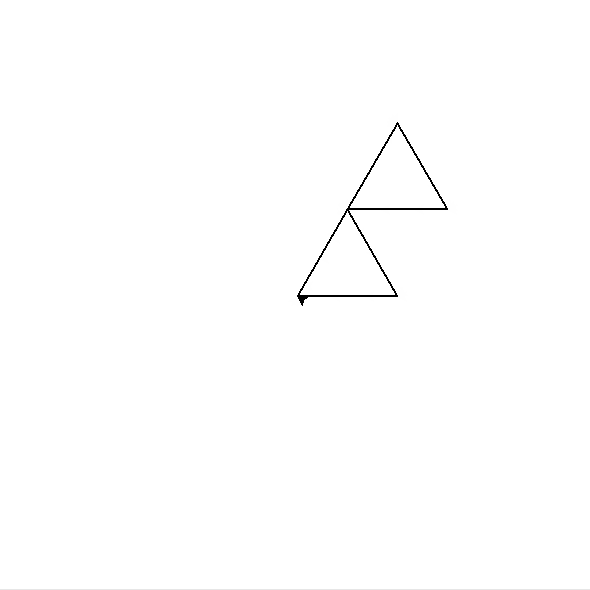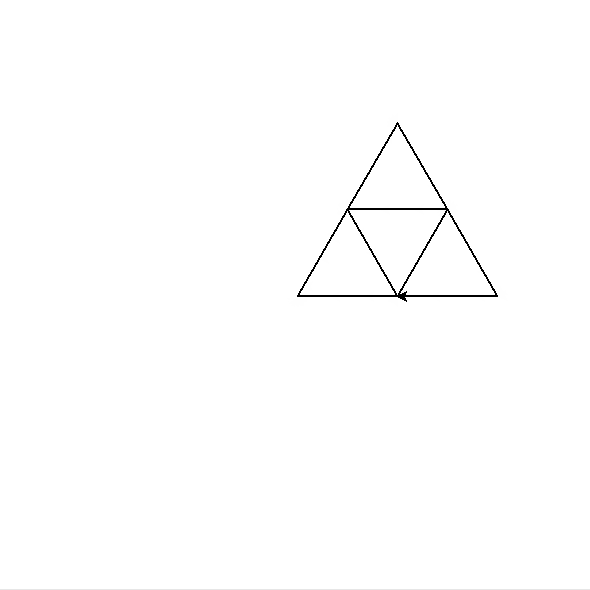
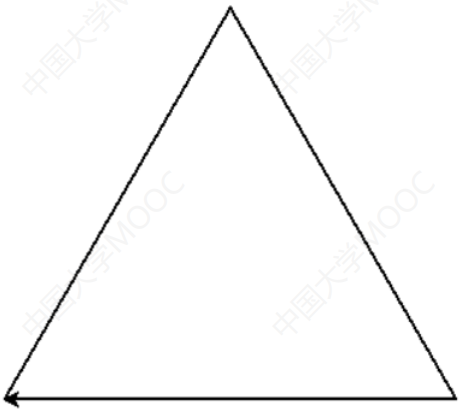
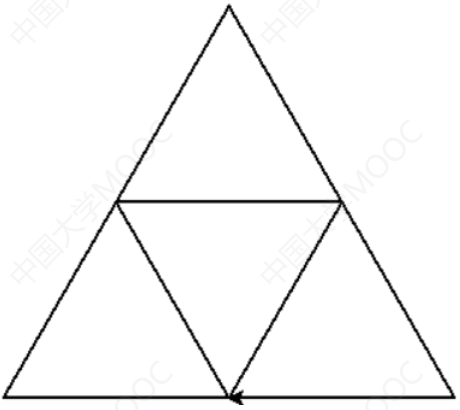
奇异三角形

一个边长为x的0阶奇异三角形，是一个边长为x的等边三角形
一个边长为x的n阶奇异三角形，是一个边长为x的等边三角形，三个角上分别是一个边长为x/2的n-1阶奇异三角形

• 0阶奇异三角形

• 1阶奇异三角形

• 2阶奇异三角形

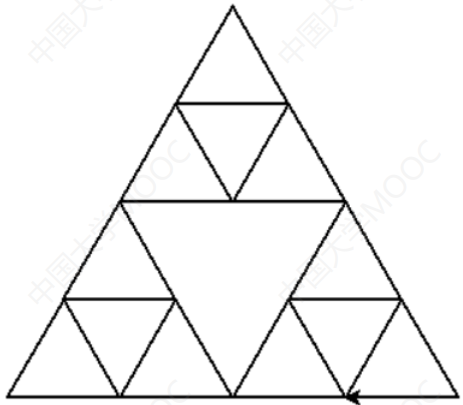
• 输入整数n，(0<=n<=5)，绘制n阶奇异三角形

• 提示

1) turtle.left(x) 可以向左拐 x 度
2) turtle.right(x)可以向右拐 x 度
3) pos = turtle.pos() 可以取得画笔当前位置， 以后 turtle.goto(pos)就可以移动画笔到那个位置
4) turtle.seth(x)可以设置画笔方向为角度 x
5) 绘图完成后调用 turtle.done() 可以保持绘图窗口

• 代码

intn = int(input())

import turtle
def san(n, x):
    if 0 == n:
        for angle in [60, -120, -120]:
            turtle.left(angle)
            turtle.fd(x)
    else:
        pos = turtle.pos()
        san(n - 1, x / 2)
        turtle.penup()

        turtle.goto(pos)  #-180
        turtle.right(120)
        turtle.fd(x / 2)
        turtle.right(60)

        turtle.pendown()
        san(n - 1, x / 2)
        turtle.penup()

        turtle.goto(pos)
        turtle.right(180)
        turtle.fd(x / 2)
        turtle.pendown()

        san(n - 1, x / 2)

turtle.setup(600, 600)
turtle.pensize(2)
san(intn, 200)
turtle.done()