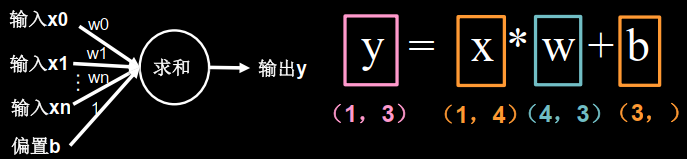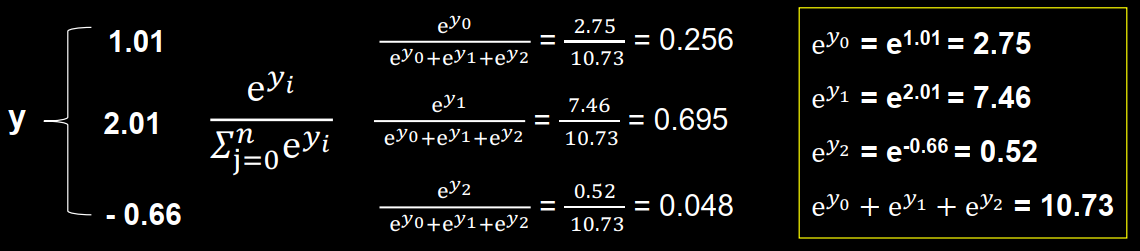人工智能实践-Tensorflow笔记-MOOC-第一讲神经网络计算

[TOC]

人工智能实践-Tensorflow笔记-MOOC-第一讲神经网络计算

本讲目标：学会神经网络计算过程，使用基于TF2原生

代码搭建你的第一个的神经网络训练模型

当今人工智能主流方向——连接主义
前向传播
损失函数（初体会）
梯度下降（初体会）
学习率（初体会）
反向传播更新参数
Tensorflow 2 常用函数

人工智能：让机器具备人的思维和意识。

人工智能三学派

我们常说的人工智能，就是让机器具备人的思维和意识。人工智能主要有三个学派，即行为主义、符号主义和连接主义。

行为主义：基于控制论，构建感知-动作控制系统。（控制论，如平衡、行走、避障等自适应控制系统）
是基于控制论的，是在构建感知、动作的控制系统。单脚站立是行为主义一个典型例子，通过感知要摔倒的方向，控制两只手的动作，保持身体的平衡。这就构建了一个感知、动作的控制系统，是典型的行为主义。
符号主义：基于算数逻辑表达式，求解问题时先把问题描述为表达式，再求解表达式。（可用公式描述、实现理性思维，如专家系统）
基于算数逻辑表达式。即在求解问题时，先把问题描述为表达式，再求解表达式。例如在求解某个问题时，利用 if case 等条件语句和若干计算公式描述出来，即使用了符号主义的方法，如专家系统。符号主义是能用公式描述的人工智能，它让计算机具备了理性思维。
连接主义：仿生学，模仿神经元连接关系。（仿脑神经元连接，实现感性思维，如神经网络）
仿造人脑内的神经元连接关系，使人类不仅具备理性思维，还具备无法用公式描述的感性思维，如对某些知识产生记忆。

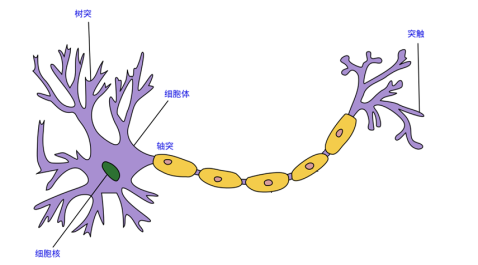
人脑中的一根神经元，其中紫色部分为树突，其作为神经元的输入。黄色部分为轴突，其作为神经元的输出。人脑就是由 860 亿个这样的神经元首尾相接组成的网络。

基于连接主义的神经网络模仿上图的神经元，使计算机具有感性思维。

随着我们的成长，大量的数据通过视觉、听觉涌入大脑，使我们的神经网络连接，也就是这些神经元连接线上的权重发生了变化，有些线上的权重增强了，有些线上的权重减弱了。

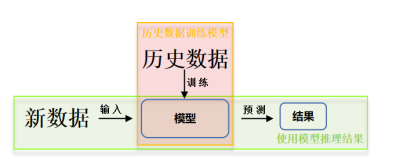
神经网络设计过程

计算机具备感性思维的几个步骤

准备数据
准备数据-标签，数量越多越好。
搭建网络
优化参数
反向传播，优化权重直到准确率达到要求。
应用网络
新数据向前传播，输出概率值最大的一个。

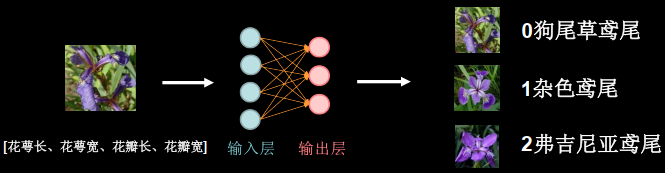
用神经网络实现鸢尾花分类

准备数据/数据集特征

人们通过经验总结出了规律：通过测量花的花萼长、花萼宽、花瓣长、花瓣宽，可以得出鸢尾花的类别。
例如：花萼长>花萼宽且花瓣长/花瓣宽>2 则为 1杂色鸢尾

if语句 case语句 —— 专家系统把专家的经验告知计算机，计算机执行逻辑判别（理性计算），给出分类。

神经网络算法：采用搭建神经网络的办法对其进行分类，即将鸢尾花花萼长、花萼宽、花瓣长、花瓣宽四个输入属性喂入搭建好的神经网络，网络优化参数得到模型，输出分类结果。

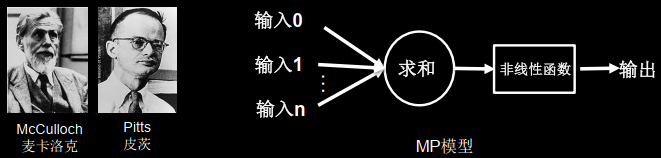
粉色小球是神经元，1943年已经提出神经元的计算模型——MP模型。

搭建网络

为本次求解简单，将MP模型中的非线性函数去掉，得到简化的MP模型。

x是1行4列的输入特征
w是4行3列的权重
b是偏置项，3个
y是1行3列的输出(三种鸢尾花的可能大小)

输入特征为标签0狗尾鸢尾

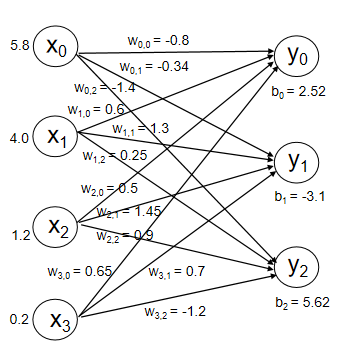
y0、y1、y2和x0、x1、x2、x3都有连接，称为全连接网络。

网络搭建完成后进行参数初始化，为随机数。

前向传播

$y = x * w +b$ $\begin{bmatrix}5.8 & 4.0 & 0.2\end{bmatrix} \tag{2} $$ * $$ \begin{bmatrix}-0.8 & -0.34 & -1.4\\ 0.6 & 1.3 & 0.25 \\ 0.5 & 1.45 & 0.9 \\ 0.65 & 0.7 & -1.2 \end{bmatrix} \tag{2} $$ + $$ \begin{bmatrix} 2.52 & -3.1 & 5.62 \end{bmatrix} \tag{2} $$ = $$ \begin{bmatrix} 1.01 & 2.01 & -0.66\end{bmatrix} \tag{2}$

这个结果发现0类的鸢尾得分不是最高的。

因为初始权重值是随机给的。

损失函数

损失函数(loss function) = 预测值（y）与标准答案（y_）的差距。

损失函数可以定量判断参数w、偏置项b的优劣，当损失函数输出最小时，参数w、偏置项b会出现最优值。

均方误差： $MSE(y, y_{\_}) = \frac{\sum_{k=0}^{n} (y-y_{\_})^{2}}{n}$

梯度下降

目的：想找到一组参数w和b，使得损失函数最小。

梯度：函数对各参数求偏导后的向量。函数梯度下降方向是函数减小方向。

梯度下降法：沿损失函数梯度下降的方向，寻找损失函数的最小值，得到最优参数的方法。

$w_{t+1} = w_{t} - lr * \frac{\partial loss}{\partial w_{t}}$ $b_{t+1} = b - lr * \frac{\partial loss}{\partial b_{t}}$ $w_{t+1} * x + b_{t+1} → y$

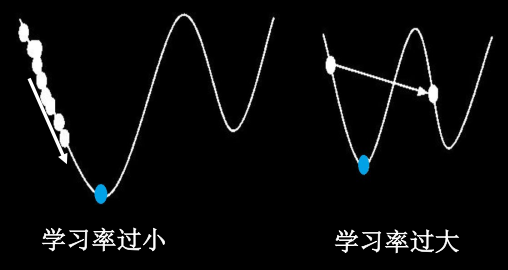
学习率（learning rate，lr）：当学习率设置过小，收敛过程将变得很缓慢。当学习率设置过大，梯度可能会在最小值附近来回震荡，甚至可能无法收敛。

反向传播

$w_{t+1} = w_{t} - lr * \frac{\partial loss}{\partial w_{t}}$

反向传播：从后向前，逐层求损失函数对每层神经元参数的偏导数，迭代更新所有参数。

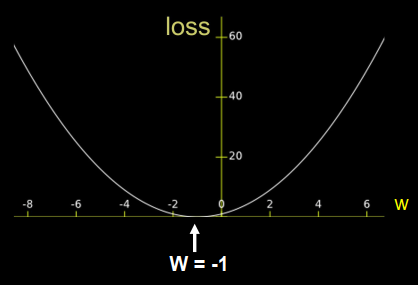
例如：损失函数 $ loss = (w+1)^{2} $， $ \frac{\partial loss}{\partial w} = 2w+2 $

参数w初始化为5，学习率为0.2，则：
1次参数w：5 5 - 0.2 ( 2 5 + 2 ) = 2.6
2次参数w：2.6 2.6 - 0.2 ( 2 2.6 +2 ) = 1.16
3次参数w：1.16 1.16 - 0.2 ( 2 1.16 + 2 ) = 0.296
4次参数w：0.296
…

目的是找到反向w=-1，损失函数最低的点

import tensorflow as tf

w = tf.Variable(tf.constant(5, dtype=tf.float32))
lr = 0.2
epoch = 40

for epoch in range(epoch):  # for epoch 定义顶层循环，表示对数据集循环epoch次，此例数据集数据仅有1个w,初始化时候constant赋值为5，循环40次迭代。
    with tf.GradientTape() as tape:  # with结构到grads框起了梯度的计算过程。
        loss = tf.square(w + 1)
    grads = tape.gradient(loss, w)  # .gradient函数告知谁对谁求导

    w.assign_sub(lr * grads)  # .assign_sub 对变量做自减 即：w -= lr*grads 即 w = w - lr*grads
    print("After %s epoch,w is %f,loss is %f" % (epoch, w.numpy(), loss))

# lr初始值：0.2   请自改学习率  0.001  0.999 看收敛过程
# 最终目的：找到 loss 最小 即 w = -1 的最优参数w

张量生成

张量(Tensor)：多维数组（列表）

阶：张量的维数

维数	阶	名字	例子
0-D	0	标量 scalar	s = 123
1-D	1	向量 vector	v = [1, 2, 3]
2-D	2	矩阵 matrix	m = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
n-D	n	张量 tensor	t = [[[.. n个

张量可以表示0阶到n阶数组（列表）

数据类型

tf.int, tf.float ......

tf.int 32, tf.float 32, tf.float 64

tf.bool

tf.constant([True, False])

tf.string

tf.constant(“Hello, world!”)

创建一个张量

tf.constant(张量内容, dtype = 数据类型(可选))

import tensorflow as tf
a = tf.constant([1, 5], dtype = tf.int64)
print(a)
print(a.dtype)
print(a.shape)

运行结果：

1
2
3

<tf.Tensor([1,5], shape=(2 ,), dtype = int64)
<dtype:'int64'>
(2,)

shape隔开1个数组说明是1纬，值为2，说明有两数字。

创建一个Tensor

将numpy的数据类型转换为Tensor数据类型

tf.convert_to_tensor(数据名, dtype = 数据类型(可选))

import tensorflow as tf
import numpy as np
a = np.arange(0, 5)
b = tf.convert_to_tensor(a, dtype = tf.int64)
print(a)
print(b)

运行结果：

1 2	[0 1 2 3 4] tf.Tensor([0 1 2 3 4], shape=(5,), dtype = int64)

纬度：
一维直接写个数
二维用[行, 列]
多维用[n, m, j, k ……]

创建全为0的张量

1	tf.zero(维度)

创建全为1的张量

1	tf.ones(纬度)

创建全为指定值的张量

1	tf.fill(纬度, 指定值)

a = tf.zeros([2, 3])
b = tf.ones(4)
c = tf.fill([2, 2], 9)
print(a)
print(b)
print(c)

运行结果

1
2
3

tf.Tensor([[0. 0. 0.][0. 0. 0.]], shape = (2, 3), dtype = float32)
tf.Tensor([1. 1. 1. 1.], shape = (4, ), dtype = float32)
tf.Tensor([[9 9][9 9]], shape = (2, 2), dtype = int32)

生成正态分布的随机数，默认均值为0，标准差为1

1	tf.random.normal(纬度, mean=均值，stddev=标准差)

生成截断式正态分布的随机数

1	tf.random.truncated_normal(纬度, mean=均值, stddev=标准差)

在tf.turncated_normal中如果随机生成数据的取值在$ (\mu - 2 \sigma, \mu +2 \sigma) $之外则重新进行生成，保证了生成值在均值附近。

$ \mu $：均值
$ \sigma $：标准差

标准差计算公式： $\sigma = \sqrt{\frac{ \sum_{i=1}^{n} (x_{i} - \bar{x})^{2}} {n}}$

d = tf.random.normal ([2, 2], mean=0.5, stddev=1)
print(d)
e = tf.random.truncated_normal ([2, 2], mean=0.5, stddev=1)
print(e)

运行结果：

tf.Tensor(
[[0.7925745 0.643315 ]
[1.4752257 0.2533372]], shape=(2, 2), dtype=float32)

tf.Tensor(
[[ 1.3688478 1.0125661 ]
[ 0.17475659 -0.02224463]], shape=(2, 2), dtype=float32)

生成均匀分布随机数[minval, maxval)

1	tf.random.uniform(维度, minval=最小值, maxval=最大值)

1 2	f = tf.random.uniform([2, 2], minval=0, maxval=1) print(f)

运行结果：

1
2
3

tf.Tensor(
[[0.28219545 0.15581512]
[0.77972126 0.47817433]], shape=(2, 2), dtype=float32)

常用函数

强制tensor转换为该数据类型

1	tf.cast(张量名, dtype=数据类型)

计算张量维度上元素的最小值

1	tf.reduce_min(张量名)

计算张量维度上元素的最大值

1	tf.reduce_max(张量名)

x1 = tf.constant([1., 2., 3.], dtype=tf.float64)
print(x1)

x2 = tf.cast(x1, tf.int32)
print(x2)
print(tf.reduce_min(x2), tf.reduce_max(x2))

运行结果：

tf.Tensor([1. 2. 3.], shape=(3,), dtype=float64)

tf.Tensor([1 2 3], shape=(3,), dtype=int32)

tf.Tensor(1, shape=(), dtype=int32)

tf.Tensor(3, shape=(), dtype=int32)

axis

在一个二维张量或数组中，可以通过调整 axis 等于0或1控制执行维度。

axis=0代表跨行（经度， down)，而axis=1代表跨列（纬度， across)
如果不指定axis，则所有元素参与计算。

计算张量沿着指定维度的平均值

1	tf.reduce_mean(张量名, axis=操作轴)

计算张量沿着指定维度的和

1	tf.reduce_sum(张量名, axis=操作轴)

案例

x=tf.constant([[1, 2, 3], [2, 2, 3]])
print(x)
print(tf.reduce_mean(x))
print(tf.reduce_sum(x, axis=1))

运行结果：

tf.Tensor(
[[1 2 3]
[2 2 3]], shape=(2, 3), dtype=int32)

tf.Tensor(2, shape=(), dtype=int32)

tf.Tensor([6 7], shape=(2,), dtype=int32)

tf.Variable

tf.Variable() 将变量标记为“可训练” ，被标记的变量会在反向传播中记录梯度信息。神经网络训练中，常用该函数标记待训练参数。

1 2	tf.Variable(初始值) w = tf.Variable(tf.random.normal([2, 2], mean=0, stddev=1))

TensorFlow中的数学运算

对应元素的四则运算： tf.add, tf.subtract, tf.multiply, tf.divide
平方、次方与开方： tf.square, tf.pow, tf.sqrt
矩阵乘： tf.matmul

对应元素的四则运算

实现两个张量的对应元素相加

1	tf.add(张量1, 张量2)

实现两个张量的对应元素相减

1	tf.subtract(张量1, 张量2)

实现两个张量的对应元素相乘

1	tf.multiply(张量1, 张量2)

实现两个张量的对应元素相除

1	tf.divide(张量1, 张量2)

只有维度相同的张量才可以做四则运算

案例

a = tf.ones([1, 3])
b = tf.fill([1, 3], 3.)
print(a)
print(b)
print(tf.add(a,b))
print(tf.subtract(a,b))
print(tf.multiply(a,b))
print(tf.divide(b,a))

运行结果

tf.Tensor([[1. 1. 1.]], shape=(1, 3), dtype=float32)

tf.Tensor([[3. 3. 3.]], shape=(1, 3), dtype=float32

tf.Tensor([[4. 4. 4.]], shape=(1, 3), dtype=float32)

tf.Tensor([[-2. -2. -2.]], shape=(1, 3), dtype=float32)

tf.Tensor([[3. 3. 3.]], shape=(1, 3), dtype=float32)

tf.Tensor([[3. 3. 3.]], shape=(1, 3), dtype=float32)

平方、次方与开方

计算某个张量的平方

1	tf.square(张量名)

计算某个张量的n次方

1	tf.pow(张量名, n次方数)

计算某个张量的开方

1	tf.sqrt(张量名）

案例

a = tf.fill([1, 2], 3.)
print(a)
print(tf.pow(a, 3))
print(tf.square(a))
print(tf.sqrt(a))

运行结果：

tf.Tensor([[3. 3.]], shape=(1, 2), dtype=float32)
tf.Tensor([[27. 27.]], shape=(1, 2), dtype=float32)
tf.Tensor([[9. 9.]], shape=(1, 2), dtype=float32)
tf.Tensor([[1.7320508 1.7320508]], shape=(1, 2), dtype=float32)

矩阵乘 tf.matmul

实现两个矩阵的相乘

1	tf.matmul(矩阵1, 矩阵2)

案例

1
2
3

a = tf.ones([3, 2])
b = tf.fill([2, 3], 3.)
print(tf.matmul(a, b))

运行结果：

[3, 2] * [2 ,3] = [3, 3]
1 1 3 3 3
1 1 3 3 3
1 1

tf.Tensor(
[[6. 6. 6.]
[6. 6. 6.]
[6. 6. 6.]], shape=(3, 3), dtype=float32)

tf.data.Dataset.from_tensor_slices

神经网络在训练时，是将输入特征和标签配对后喂入网络的。

切分传入张量的第一维度，生成输入特征/标签对，构建数据集

1	data = tf.data.Dataset.from_tensor_slices((输入特征, 标签))

（Numpy和Tensor格式都可用该语句读入数据）

案例

# 收集特征
features = tf.constant([12,23,10,17])
# 对应标签
labels = tf.constant([0, 1, 1, 0])
# 打特征和标签
dataset = tf.data.Dataset.from_tensor_slices((features, labels))

print(dataset)

for element in dataset:
	print(element)

运行结果：

# (特征, 标签) 配对
<TensorSliceDataset shapes: ((), ()), types: (tf.int32, tf.int32))>

(<tf.Tensor: id=9, shape=(), dtype=int32, numpy=12>, <tf.Tensor: id=10, shape=(), dtype=int32, numpy=0>)

(<tf.Tensor: id=11, shape=(), dtype=int32, numpy=23>, <tf.Tensor: id=12, shape=(), dtype=int32, numpy=1>)

(<tf.Tensor: id=13, shape=(), dtype=int32, numpy=10>, <tf.Tensor: id=14, shape=(), dtype=int32, numpy=1>)

(<tf.Tensor: id=15, shape=(), dtype=int32, numpy=17>, <tf.Tensor: id=16, shape=(), dtype=int32, numpy=0>)

张量梯度求导tf.GradientTape

with 结构中使用来实现对指定参数的求导运算
with 结构记录计算过程， gradient求出张量的梯度

1
2
3

with tf.GradientTape( ) as tape:
	若干个计算过程
grad=tape.gradient(函数, 对谁求导)

案例

with tf.GradientTape( ) as tape:
	w = tf.Variable(tf.constant(3.0))
	loss = tf.pow(w,2) #loss=w^2 loss’=2w
grad = tape.gradient(loss,w)
print(grad)

$\frac{ \sigma w^{2} } { \sigma w } = 2 w = 2 * 3.0 = 6.0$

运行结果

1	tf.Tensor(6.0, shape=(), dtype=float32)

枚举enumerate

enumerate是python的内建函数，它可遍历每个元素(如列表、元组或字符串)，组合为：索引元素，常在for循环中使用。

可以在元素前配上对应的索引号

enumerate(列表名)

1
2
3

seq = ['one', 'two', 'three']
for i, element in enumerate(seq):
	print(i, element)

运行结果

1
2
3

0 one
1 two
2 three

独热编码tf.one_hot

独热编码（one-hot encoding：在分类问题中，常用独热码做标签，标记类别： 1表示是， 0表示非。

例如：0狗尾草鸢尾 1杂色鸢尾 2弗吉尼亚鸢尾三种
对于标签1，对应独热码是(0. 1. 0.)

即标签1，0%概率是0狗尾草鸢尾，100%概率是1杂色鸢尾，0%概率是2弗吉尼亚鸢尾

tf.one_hot()函数将待转换数据，转换为one-hot形式的数据输出。

1	tf.one_hot(待转换数据, depth=几分类)

案例

classes = 3
labels = tf.constant([1, 0, 2]) # 输入的元素值最小为0, 最大为2
output = tf.one_hot(labels, depth=classes)
print(output)

运行结果：

1
2
3

[[0. 1. 0.]
[1. 0. 0.]
[0. 0. 1.]], shape=(3, 3), dtype=float32)

正态分布tf.nn.softmax

神经网络完成前向传播，计算出了每一种类型的可能性大小，数字在符合概率分布后才可以和独热码的标签作比较。

$Softmax(y_{i}) = \frac{e^{y_{i}}}{\sum_{j=0}^{n} e^{y_{i}}}$

tf.nn.softmax(x) 使输出符合概率分布

当n分类的n个输出

$( y_{ 0 }, y_{1}, ……, y_{ n - 1})$

通过 softmax() 函数，便符合概率分布了。

即每个输出值变为0~1之间的概率值。

$\forall x P(X = x) \in [0, 1] $$ 且 $$ \sum_{x} P(X = x) = 1$

案例

1
2
3

y = tf.constant ( [1.01, 2.01, -0.66] )
y_pro = tf.nn.softmax(y)
print("After softmax, y_pro is:", y_pro)

输出结果：

1	After softmax, y_pro is: tf.Tensor([0.25598174 0.69583046 0.0481878], shape=(3, ), dtype=float32)

参数自更新assign_sub

赋值操作，更新参数的值并返回。
调用assign_sub前，先用tf.Variable定义变量 w 为可训练（可自更新）。

1	w.assign_sub(w要自减的内容)

案例

w = tf.Variable(4)

# w -= 1 即 w = w - 1
w.assign_sub(1)

print(w)

运行结果：

1	<tf.Variable 'Variable:0' shape=() dtype=int32, numpy=3>

返回最大索引tf.argmax

返回张量沿指定维度最大值的索引

1
2
3

# axis=0经度，纵向列
# axis=1纬度，横向行
tf.argmax(张量名, axis=操作轴)

案例

import numpy as np

test = np.array(
[[1, 2, 3], 
[2, 3, 4], 
[5, 4, 3], 
[8, 7, 2]])

print(test)
print(tf.argmax(test, axis=0)) #返回每一列（经度）最大值的索引
print(tf.argmax(test, axis=1)) #返回每一行（纬度）最大值的索引

运行结果：

[[1 2 3]
[2 3 4]
[5 4 3]
[8 7 2]]

tf.Tensor([3 3 1], shape=(3, ), dtype=int64)
tf.Tensor([2 2 0 0], shape=(4, ), dtype=int64)

鸢尾花数据集读入

数据集介绍

共有数据150组，每组包括花萼长、花萼宽、花瓣长、花瓣宽4个输入特征。
同时给出了，这一组特征对应的鸢尾花类别。
类别包括Setosa Iris（狗尾草鸢尾）， Versicolour Iris（杂色鸢尾）， Virginica Iris（弗吉尼亚鸢尾）三类，分别用数字0， 1， 2表示。

读入数据集

从sklearn包datasets读入数据集，语法为：

1
2
3

from sklearn.datasets import load_iris
x_data = datasets.load_iris().data # 返回iris数据集所有输入特征
y_data = datasets.load_iris().target # 返回iris数据集所有标签

from sklearn import datasets
from pandas import DataFrame
import pandas as pd

x_data = datasets.load_iris().data  # .data返回iris数据集所有输入特征
y_data = datasets.load_iris().target  # .target返回iris数据集所有标签
print("x_data from datasets: \n", x_data)
print("y_data from datasets: \n", y_data)

x_data = DataFrame(x_data, columns=['花萼长度', '花萼宽度', '花瓣长度', '花瓣宽度']) # 为表格增加行索引（左侧）和列标签（上方）
pd.set_option('display.unicode.east_asian_width', True)  # 设置列名对齐
print("x_data add index: \n", x_data)

x_data['类别'] = y_data  # 新加一列，列标签为‘类别’，数据为y_data
print("x_data add a column: \n", x_data)

#类型维度不确定时，建议用print函数打印出来确认效果

x_data from datasets: 
 [[5.1 3.5 1.4 0.2]
 [4.9 3.  1.4 0.2]
 [4.7 3.2 1.3 0.2]
 [4.6 3.1 1.5 0.2]
 [5.  3.6 1.4 0.2]
 [5.4 3.9 1.7 0.4]
 [4.6 3.4 1.4 0.3]
 [5.  3.4 1.5 0.2]
 [4.4 2.9 1.4 0.2]
 [4.9 3.1 1.5 0.1]
 [5.4 3.7 1.5 0.2]
 [4.8 3.4 1.6 0.2]
 [4.8 3.  1.4 0.1]
 [4.3 3.  1.1 0.1]
 [5.8 4.  1.2 0.2]
 [5.7 4.4 1.5 0.4]
 [5.4 3.9 1.3 0.4]
 [5.1 3.5 1.4 0.3]
 [5.7 3.8 1.7 0.3]
 [5.1 3.8 1.5 0.3]
 [5.4 3.4 1.7 0.2]
 [5.1 3.7 1.5 0.4]
 [4.6 3.6 1.  0.2]
 [5.1 3.3 1.7 0.5]
 [4.8 3.4 1.9 0.2]
 [5.  3.  1.6 0.2]
 [5.  3.4 1.6 0.4]
 [5.2 3.5 1.5 0.2]
 [5.2 3.4 1.4 0.2]
 [4.7 3.2 1.6 0.2]
 [4.8 3.1 1.6 0.2]
 [5.4 3.4 1.5 0.4]
 [5.2 4.1 1.5 0.1]
 [5.5 4.2 1.4 0.2]
 [4.9 3.1 1.5 0.2]
 [5.  3.2 1.2 0.2]
 [5.5 3.5 1.3 0.2]
 [4.9 3.6 1.4 0.1]
 [4.4 3.  1.3 0.2]
 [5.1 3.4 1.5 0.2]
 [5.  3.5 1.3 0.3]
 [4.5 2.3 1.3 0.3]
 [4.4 3.2 1.3 0.2]
 [5.  3.5 1.6 0.6]
 [5.1 3.8 1.9 0.4]
 [4.8 3.  1.4 0.3]
 [5.1 3.8 1.6 0.2]
 [4.6 3.2 1.4 0.2]
 [5.3 3.7 1.5 0.2]
 [5.  3.3 1.4 0.2]
 [7.  3.2 4.7 1.4]
 [6.4 3.2 4.5 1.5]
 [6.9 3.1 4.9 1.5]
 [5.5 2.3 4.  1.3]
 [6.5 2.8 4.6 1.5]
 [5.7 2.8 4.5 1.3]
 [6.3 3.3 4.7 1.6]
 [4.9 2.4 3.3 1. ]
 [6.6 2.9 4.6 1.3]
 [5.2 2.7 3.9 1.4]
 [5.  2.  3.5 1. ]
 [5.9 3.  4.2 1.5]
 [6.  2.2 4.  1. ]
 [6.1 2.9 4.7 1.4]
 [5.6 2.9 3.6 1.3]
 [6.7 3.1 4.4 1.4]
 [5.6 3.  4.5 1.5]
 [5.8 2.7 4.1 1. ]
 [6.2 2.2 4.5 1.5]
 [5.6 2.5 3.9 1.1]
 [5.9 3.2 4.8 1.8]
 [6.1 2.8 4.  1.3]
 [6.3 2.5 4.9 1.5]
 [6.1 2.8 4.7 1.2]
 [6.4 2.9 4.3 1.3]
 [6.6 3.  4.4 1.4]
 [6.8 2.8 4.8 1.4]
 [6.7 3.  5.  1.7]
 [6.  2.9 4.5 1.5]
 [5.7 2.6 3.5 1. ]
 [5.5 2.4 3.8 1.1]
 [5.5 2.4 3.7 1. ]
 [5.8 2.7 3.9 1.2]
 [6.  2.7 5.1 1.6]
 [5.4 3.  4.5 1.5]
 [6.  3.4 4.5 1.6]
 [6.7 3.1 4.7 1.5]
 [6.3 2.3 4.4 1.3]
 [5.6 3.  4.1 1.3]
 [5.5 2.5 4.  1.3]
 [5.5 2.6 4.4 1.2]
 [6.1 3.  4.6 1.4]
 [5.8 2.6 4.  1.2]
 [5.  2.3 3.3 1. ]
 [5.6 2.7 4.2 1.3]
 [5.7 3.  4.2 1.2]
 [5.7 2.9 4.2 1.3]
 [6.2 2.9 4.3 1.3]
 [5.1 2.5 3.  1.1]
 [5.7 2.8 4.1 1.3]
 [6.3 3.3 6.  2.5]
 [5.8 2.7 5.1 1.9]
 [7.1 3.  5.9 2.1]
 [6.3 2.9 5.6 1.8]
 [6.5 3.  5.8 2.2]
 [7.6 3.  6.6 2.1]
 [4.9 2.5 4.5 1.7]
 [7.3 2.9 6.3 1.8]
 [6.7 2.5 5.8 1.8]
 [7.2 3.6 6.1 2.5]
 [6.5 3.2 5.1 2. ]
 [6.4 2.7 5.3 1.9]
 [6.8 3.  5.5 2.1]
 [5.7 2.5 5.  2. ]
 [5.8 2.8 5.1 2.4]
 [6.4 3.2 5.3 2.3]
 [6.5 3.  5.5 1.8]
 [7.7 3.8 6.7 2.2]
 [7.7 2.6 6.9 2.3]
 [6.  2.2 5.  1.5]
 [6.9 3.2 5.7 2.3]
 [5.6 2.8 4.9 2. ]
 [7.7 2.8 6.7 2. ]
 [6.3 2.7 4.9 1.8]
 [6.7 3.3 5.7 2.1]
 [7.2 3.2 6.  1.8]
 [6.2 2.8 4.8 1.8]
 [6.1 3.  4.9 1.8]
 [6.4 2.8 5.6 2.1]
 [7.2 3.  5.8 1.6]
 [7.4 2.8 6.1 1.9]
 [7.9 3.8 6.4 2. ]
 [6.4 2.8 5.6 2.2]
 [6.3 2.8 5.1 1.5]
 [6.1 2.6 5.6 1.4]
 [7.7 3.  6.1 2.3]
 [6.3 3.4 5.6 2.4]
 [6.4 3.1 5.5 1.8]
 [6.  3.  4.8 1.8]
 [6.9 3.1 5.4 2.1]
 [6.7 3.1 5.6 2.4]
 [6.9 3.1 5.1 2.3]
 [5.8 2.7 5.1 1.9]
 [6.8 3.2 5.9 2.3]
 [6.7 3.3 5.7 2.5]
 [6.7 3.  5.2 2.3]
 [6.3 2.5 5.  1.9]
 [6.5 3.  5.2 2. ]
 [6.2 3.4 5.4 2.3]
 [5.9 3.  5.1 1.8]]
y_data from datasets: 
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]
x_data add index: 
      花萼长度  花萼宽度  花瓣长度  花瓣宽度
0         5.1       3.5       1.4       0.2
1         4.9       3.0       1.4       0.2
2         4.7       3.2       1.3       0.2
3         4.6       3.1       1.5       0.2
4         5.0       3.6       1.4       0.2
..        ...       ...       ...       ...
145       6.7       3.0       5.2       2.3
146       6.3       2.5       5.0       1.9
147       6.5       3.0       5.2       2.0
148       6.2       3.4       5.4       2.3
149       5.9       3.0       5.1       1.8
[150 rows x 4 columns]
x_data add a column: 
      花萼长度  花萼宽度  花瓣长度  花瓣宽度  类别
0         5.1       3.5       1.4       0.2     0
1         4.9       3.0       1.4       0.2     0
2         4.7       3.2       1.3       0.2     0
3         4.6       3.1       1.5       0.2     0
4         5.0       3.6       1.4       0.2     0
..        ...       ...       ...       ...   ...
145       6.7       3.0       5.2       2.3     2
146       6.3       2.5       5.0       1.9     2
147       6.5       3.0       5.2       2.0     2
148       6.2       3.4       5.4       2.3     2
149       5.9       3.0       5.1       1.8     2
[150 rows x 5 columns]

神经网络实现鸢尾花分类

准备数据

数据集读入

从sklearn包datasets 读入数据集：

1
2
3

from sklearn.datasets import datasets
x_data = datasets.load_iris().data # 返回iris数据集所有输入特征
y_data = datasets.load_iris().target # 返回iris数据集所有标签

数据集乱序

np.random.seed(116) # 使用相同的seed，使输入特征/标签一一对应
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)

生成训练集和测试集（即 x_train / y_train , x_test / y_test）

x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]

配成（输入特征，标签）对，每次读入一小撮（batch）

1 2	train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32) test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)

搭建网络

定义神经网路中所有可训练参数

1 2	w1 = tf.Variable(tf.random.truncated_normal([ 4, 3 ], stddev=0.1, seed=1)) b1 = tf.Variable(tf.random.truncated_normal([ 3 ], stddev=0.1, seed=1))

参数优化

嵌套循环迭代， with结构更新参数，显示当前loss

for epoch in range(epoch): #数据集级别迭代
    for step, (x_train, y_train) in enumerate (train_db): #batch级别迭代
        with tf.GradientTape() as tape: # 记录梯度信息
        # 前向传播过程计算y
        # 计算总loss
        grads = tape.gradient(loss, [ w1, b1 ])
        w1.assign_sub(lr * grads[0]) #参数自更新
        b1.assign_sub(lr * grads[1])
	print("Epoch {}, loss: {}".format(epoch, loss_all/4))

测试效果

计算当前参数前向传播后的准确率，显示当前acc

for x_test, y_test in test_db:
    y = tf.matmul(h, w) + b # y为预测结果
    y = tf.nn.softmax(y) # y符合概率分布
    pred = tf.argmax(y, axis=1) # 返回y中最大值的索引，即预测的分类
    pred = tf.cast(pred, dtype=y_test.dtype) #调整数据类型与标签一致
    correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
    correct = tf.reduce_sum (correct) # 将每个batch的correct数加起来
    total_correct += int (correct) # 将所有batch中的correct数加起来
    total_number += x_test.shape [0]
acc = total_correct / total_number
print("test_acc:", acc)

acc / loss可视化

plt.title('Acc Curve') # 图片标题
plt.xlabel('Epoch') # x轴名称
plt.ylabel('Acc') # y轴名称
plt.plot(test_acc, label="$Accuracy$") # 逐点画出test_acc值并连线
plt.legend()
plt.show()

安装tensorflow

1、安装Anaconda（Python3.7版本）
2、安装Pycharm
3、打开Anaconda Powershell Prompt
4、安装软件包

conda create -n TF2.1 python=3.7

conda activate TF2.1
conda install cudatoolkit=10.1

conda install cudnn=7.6

pip install tensorflow==2.1

python
import tensorflow as tf
tf.__version__

5、配置Pycharm

6、使用GPU

前提在本机安装nvidia驱动和cuda版本，CUDA版本向下兼容，可以安装最新的。

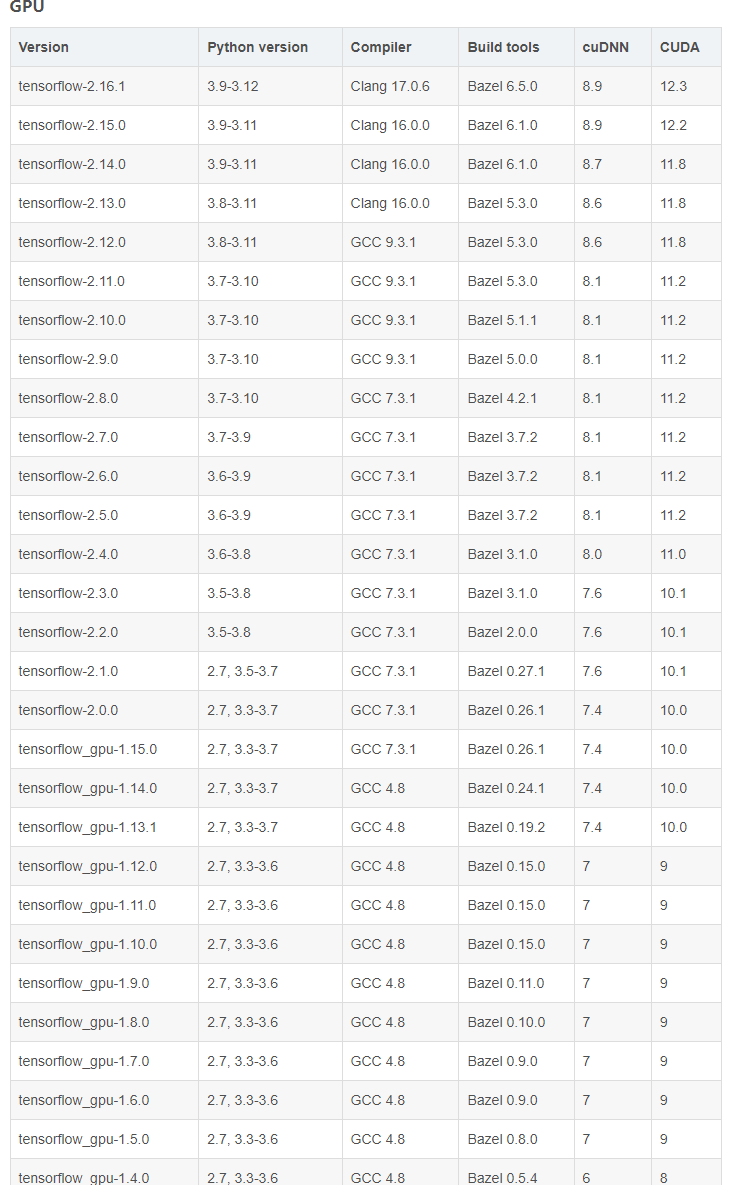
tensorflow-gpu对应python,cuda,cudnn版本查看链接

在conda虚拟环境中安装CUDA驱动库。
python3.7
tensorflow2.1
cudatoolkit10.1
cudnn7.6

conda install cudatoolkit=10.1
conda install cudnn=7.6
conda install tensorflow-gpu==2.1

pip install --upgrade keras

保险起见，可以先定cuda号然后让conda搜索

conda search tensorflow-gpu
conda install tensorflow-gpu==?.?.?
# 或者直接让conda解决
conda install tensorflow-gpu

运行测试：

import tensorflow as tf

if __name__ == '__main__':
    print('tf version: {}'.format(tf.__version__))
    print('keras version: {}'.format(tf.keras.__version__))
    # print('GPU: {}'.format(tf.test.is_gpu_available())) # 1.x版本的TF使用此行
    print('GPU: {}'.format(tf.config.list_physical_devices('GPU'))) # 2.x版本的TF使用

人工智能实践-Tensorflow笔记-MOOC-第一讲神经网络计算

本讲目标：学会神经网络计算过程，使用基于TF2原生

人工智能三学派

神经网络设计过程

用神经网络实现鸢尾花分类

准备数据/数据集特征

搭建网络

前向传播

损失函数

梯度下降

反向传播

张量生成

数据类型

创建一个张量

创建一个Tensor

将numpy的数据类型转换为Tensor数据类型

创建全为0的张量

创建全为1的张量

创建全为指定值的张量

生成正态分布的随机数，默认均值为0，标准差为1

生成截断式正态分布的随机数

生成均匀分布随机数[minval, maxval)

常用函数

强制tensor转换为该数据类型

计算张量维度上元素的最小值

计算张量维度上元素的最大值

axis

计算张量沿着指定维度的平均值

计算张量沿着指定维度的和

tf.Variable

TensorFlow中的数学运算

对应元素的四则运算

平方、次方与开方

矩阵乘 tf.matmul

tf.data.Dataset.from_tensor_slices

切分传入张量的第一维度，生成输入特征/标签对，构建数据集

张量梯度求导tf.GradientTape

枚举enumerate

独热编码tf.one_hot

正态分布tf.nn.softmax

参数自更新assign_sub

返回最大索引tf.argmax

鸢尾花数据集读入

数据集介绍

读入数据集

神经网络实现鸢尾花分类

准备数据

数据集读入

数据集乱序

生成训练集和测试集（即 x_train / y_train , x_test / y_test）

配成 （输入特征，标签） 对，每次读入一小撮（batch）

搭建网络

定义神经网路中所有可训练参数

参数优化

嵌套循环迭代， with结构更新参数，显示当前loss

测试效果

计算当前参数前向传播后的准确率，显示当前acc

acc / loss可视化

安装tensorflow

配成（输入特征，标签）对，每次读入一小撮（batch）