人工智能实践-Tensorflow笔记-MOOC-第五讲卷积神经网络

[TOC]

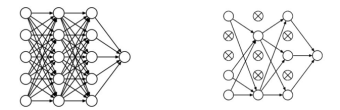
人工智能实践-Tensorflow笔记-MOOC-第五讲卷积神经网络

卷积核计算过程

全连接NN：每个神经元与前后相邻层的每一个神经元都有连接关系，输入是特征，输出为预测的结果。

全连接网络对识别和预测都有非常好的效果，可以实现分类和预测。

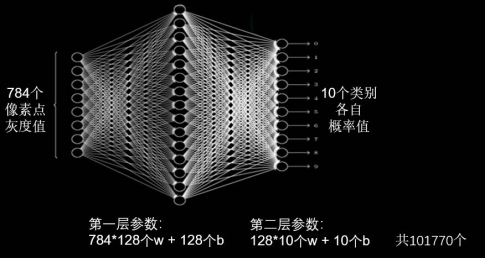
全连接网络的参数个数为：$\sum_{各层}(前层×后层+后层)$

如下图所示，针对一张分辨率仅为 28 28 的黑白图像（像素值个数为 28 28 * 1 = 784），全连接网络的参数总量就有将近 10 万个。

在实际应用中，图像的分辨率远高于此，且大多数是彩色图像，如下图所示。

虽然全连接网络一般被认为是分类预测的最佳网络，但待优化的参数过多，容易导致模型过拟合。

为了解决参数量过大而导致模型过拟合的问题，一般不会将原始图像直接输入，而是先对图像进行特征提取，再将提取到的特征输入全连接网络，如下图所示，就是将汽车图片经过多次特征提取后再喂入全连接网络。

• 卷积计算可认为是一种有效提取图像特征的方法。
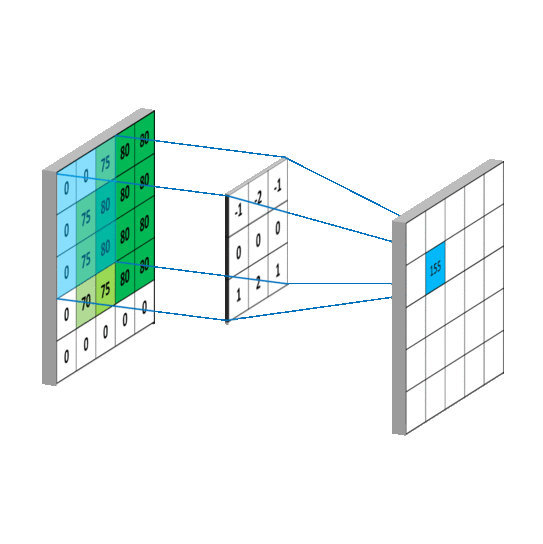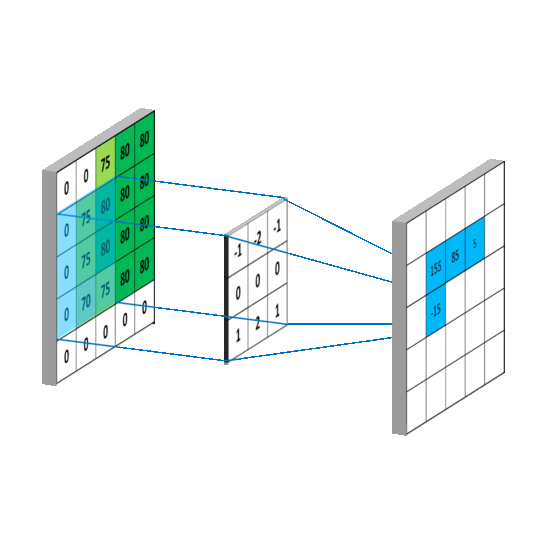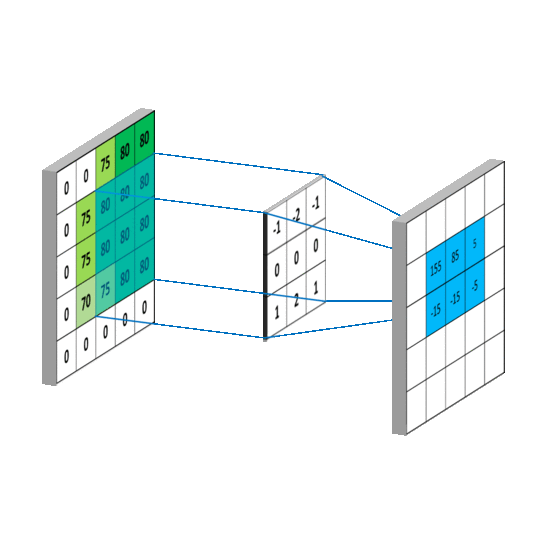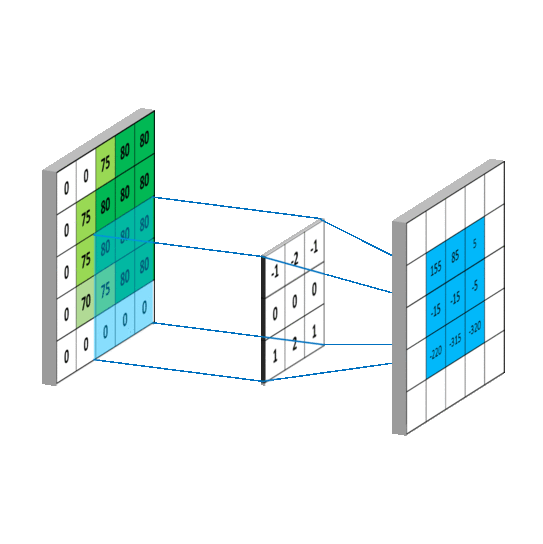
• 一般会用一个正方形的卷积核，按指定步长， 在输入特征图上滑动， 遍历输入特征图中的每个像素点。每一个步长，卷积核会与输入特征图出现重合区域，重合区域对应元素相乘、求和再加上偏置项得到输出特征的一个像素点。

如果输入是灰度图，使用单通道卷积核。

如果输入特征是三通道彩色图，可以使用 3 3 3 的卷积核，或者 5 5 3 的卷积核。

要使卷积核的通道数与输入特征图的通道数一致，要想卷积核与输入特征图对应点匹配上，必须让卷积核的深度与输入特征图的深度一致。

输入特征图的深度（channel数），决定了当前层卷积核的深度；

由于每个卷积核在卷积计算后会得到一张输出特征图，当前层使用了几个卷积核，就有几张输出特征图；当前层卷积核的个数，决定了当前层输出特征图的深度。

如果某层模型的特征提取能力不足，可以在这一层多用几个卷积核提高这一层的特征提取能力。

每一个小颗粒都存储一个带训练的参数。在执行卷积计算时，卷积核里的参数都是固定的。在每次反向传播时，这些小颗粒中存储的带训练参数，会被梯度下降法更新，卷积就是利用立体卷积核，实现了参数的空间共享。

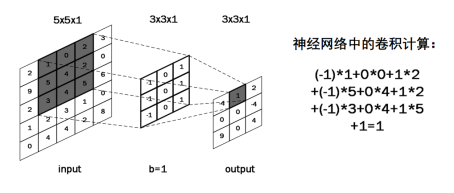
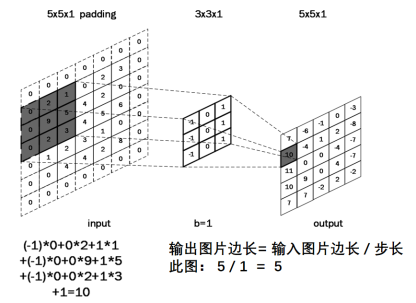
对于输入图是单通道的，选择单通道卷积核，这个例子的输入特征图是5行5列单通道，选用3 * 3单通道卷积核，滑动步长是1，在输入图上滑动，每滑动一步，输入特征图与卷积核里的9个元素重合，他们对应元素相乘求和再加上偏置项b

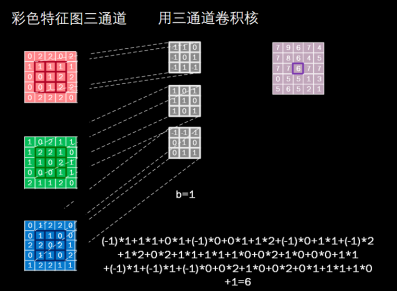
对于输入特征图是三通道的，选择3通道卷积核，该例子输入特征图是5行5列红绿蓝三通道数据，选用3 * 3 三通道卷积核，滑动步长是1，在这个输入特征上滑动，每滑动一步，输入特征图与卷积核里的27个元素重合，对应元素相乘再加上偏置项b，得到输出特则图中的一个像素值。

卷积核在输入特征图上按指定步长滑动，每个步长，卷积核会与输入特征图上部分像素点重合，重合区域，输入特征图与卷积核对应元素相乘求和，得到输出特征图中的一个像素点，当输入特征图被遍历完成，得到一张输出特征图，完成了一个卷积核的卷积计算过程。当有n个卷积核时，会有n张输出特征图，叠加在这张输出特征图的后边。
来源：https://mlnotebook.github.io/post/CNN1/

输出特征尺寸计算： 在了解神经网络中卷积计算的整个过程后， 就可以对输出特征图的尺寸进行计算，如上图所示， 5 × 5 的图像经过 3 × 3 大小的卷积核做卷积计算后输出特征尺寸为 3 × 3。

感受野

感受野（Receptive Field）：卷积神经网络各输出特征图中的每个像素点，在原始输入图片上映射区域的大小。

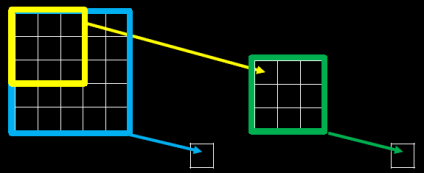
如果对 5 5 的原始图片用黄色的 3 3 卷积核作用，会输出绿色这样一个 3 3 的输出特征图，输出特征图上的每个像素点，映射到原始图片是 3 3 的区域，所以它的感受野是3。

对 3 3 的特征图用绿色的 3 3卷积核作用，会输出一个 1 1 的输出特征图，该输出特征的像素点，映射到原始图片是 5 5 的区域，其感受野是5。

如果对 5 5 的原始图片直接用蓝色的 5 5 卷积核作用，会输出一个 1 1 的输出特征图，这个像素点映射到原始输入图片是 5 5 的区域，其感受野是5。

同样一个 5 5 的原始图片，经过两层 3 3 的卷积核作用，和经过一层 5 5 的卷积核作用，都得到一个感受野是 5 的输出特征图，这两层 3 3 卷积核和一层 5 * 5 卷积核的特征提取能力是一样的。

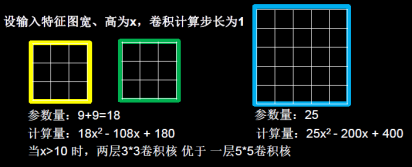
对于两层 3 3 的卷积核与一层 5 5 的卷积核的选取，需要考虑带训练参数量和计算量。

假设输入特征图宽、高为x，卷积计算步长为1。显然，两个 3 3 卷积核的参数量为 9 + 9 = 18，小于 5 5 卷积核的 25，前者的参数量更少。

对于两层 3 3 卷积核计算，待训练参数共有18个，每个 3 3 1 的卷积核计算得到一个输出像素点，需要9次乘加计算，两层 3 3 卷积核共需要 $18 x^{2} - 108 x + 180$ 次的乘加计算。第一个 3 3 卷积核输出特征图共有 $(x – 3 + 1)^2$ 个像素点，每个像素点需要进行 3 3 = 9 次乘加运算， 第二个 3 3 卷积核输出特征图共有 $(x – 3 + 1 – 3 + 1)^2$个像素点， 每个像素点同样需要进行 9 次乘加运算，总计算量为 $$ 9 (x – 3 + 1)^2 + 9 * (x – 3 + 1 – 3 + 1)^2 = 18 x^2 – 108x + 180 $$。

对于一层 5 5 卷积核计算，待训练参数共有25个，每个 5 5 1 的卷积核计算得到一个输出像素点，需要25次乘加计算，一层 5 5 卷积核，共需要 $25 x^{2} - 200 x + 400$ 次乘加计算。输出特征图共有 $(x – 5 + 1)^2$ 个像素点， 每个像素点需要进行 5 5 = 25 次乘加运算，总计算量为 $$ 25 (x – 5 + 1)^2 = 25x^2 – 200x + 400 $$ 。

当输入特征图边长大于10个像素点时，两层 3 3 卷积核比一层 5 5 卷积性能要好，这也就是为什么现在的神经网络在卷积计算中常使用两层 3 3 卷积核替换一层 5 5 卷积核的原因。

对二者的总计算量（乘加运算的次数） 进行对比，$18 x^2 – 200x + 400 < 25x^2 – 200x + 400$ ，经过简单数学运算可得 $x < 22/7 or x > 10$， x 作为特征图的边长，在大多数情况下显然会是一个大于 10 的值（非常简单的 MNIST 数据集的尺寸也达到了 28 28），所以两层 3 3 卷积核的参数量和计算量，在通常情况下都优于一层 5 5 卷积核，尤其是当特征图尺寸比较大的情况下，两层 3 3 卷积核在计算量上的优势会更加明显。

全零填充

卷积计算保持输入特征图的尺寸不变，可以使用全零填充，在输入特征图周围填充0。

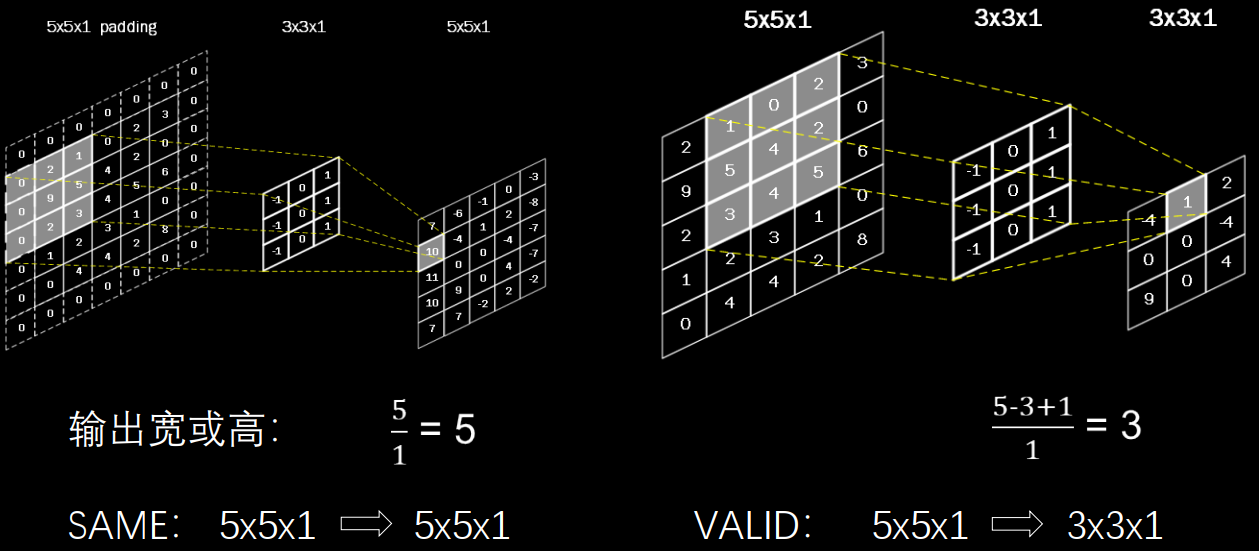
如图所示，在 5×5×1 的输入图像周围填 0，在通过 3×3×1的卷积核，进行步长为1的卷积计算，输出特征图仍是 5×5×1。

在 Tensorflow 框架中， 用参数 padding = 'SAME' 或 padding = 'VALID' 表示是否进行全零填充，其对输出特征尺寸大小的影响如下：

$$padding \left\{ \begin{array} & SAME(全0填充) & \frac{入长}{步长} (向上取整) \\ VALID(不全0填充) & \frac{入长 - 核长 + 1}{步长} (向上取整) \end{array} \right.$$

上下两行分别代表对输入图像进行全零填充或不进行填充， 对于 5×5×1 的图像来说，当 padding = 'SAME' 时， 步长是1，输出图像边长为 5 / 1 = 5； 当 padding = 'VALID' 时， 核长是3，步长是1，输出图像边长为 (5 - 3 + 1) / 1 = 3。

TF描述卷积计算层

tf.keras.layers.Conv2D(	
	filters = 卷积核个数,
	kernel_size = 卷积核尺寸,	#正方形写核长整数，或（核高h，核宽w）
	strides = 卷积步长,	#横纵向相同写步长整数，或(纵向步长h，横向步长w)，默认1
	padding = ‘SAME’ or ‘VALID’,	#使用全零填充是“same”，不使用“valid”（默认）
	activation = ‘relu’ or ‘sigmoid’ or ‘tanh’ or ‘softmax’等 #使用什么激活函数，如果这一层卷积后还有批标准化操作，不在这里进行激活，如有 BN 则此处不用写
	input_shape = (高, 宽, 通道数), #输入特征图纬度，可以省略仅在第一层有
)

# 描述三层卷积计算，每一层用自己的表述形式
model = tf.keras.models.Sequential([
    Conv2D(6, 5, padding='valid', activation='sigmoid'),##
    MaxPool2D(2, 2),
    
    Conv2D(6, (5, 5), padding='valid', activation='sigmoid'),##
    MaxPool2D(2, (2, 2)),
    
    Conv2D(filters=6, kernel_size=(5, 5), padding='valid', activation='sigmoid'),	##关键字传递参数，可读性更强
    
    MaxPool2D(pool_size=(2, 2), strides=2),
    Flatten(),
    Dense(10, activation='softmax')
])

使用此函数构建卷积层时，需要给出的信息有：
A） 输入图像的信息，即宽高和通道数；
B） 卷积核的个数以及尺寸，如 filters = 16, kernel_size = (3, 3)代表采用 16 个大小为 3×3 的
卷积核；
C） 卷积步长，即卷积核在输入图像上滑动的步长，纵向步长与横向步长通常是相同的，默
认值为 1；
D） 是否进行全零填充，全零填充的具体作用上文有描述；
E） 采用哪种激活函数，例如 relu、 softmax 等，各种函数的具体效果在前面章节中有详细描述；
这里需要注意的是，在利用 Tensorflow 框架构建卷积网络时，一般会利用 BatchNormalization
函数来构建 BN 层，进行批归一化操作，所以在 Conv2D 函数中经常不写 BN。 BN 操作的
具体含义和作用见下文。

批标准化(Batch Normalization, BN)

神经网络对0附近的数据更敏感，但是随着网络层数的增加，特征数据会出现偏离0均值的情况，标准化可以使数据符合以0为均值，1为标准差的标准正态分布。把偏移的特征数据重新拉回到0附近，常用在卷积操作和激活操作之间。

标准化：使数据符合0均值，1为标准差的分布。

批标准化：对一小批数据（batch），做标准化处理。

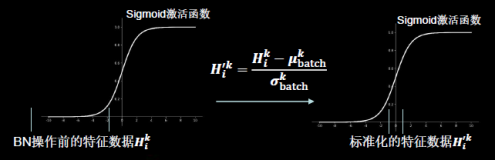
批标准化后，第k个卷积核的输出特征图（feature map）中第i个像素点。

可以通过以下公式计算批标准化后的输出特征图：

$$H_{i}^{’k} = \frac {H_{i}^{k} - \mu_{batch}^{k} } { \sigma_{batch}^{k} }$$

$ H{i}^{k} $ ：批标准化前，第k个卷积核，输出特征图中第 i 个像素点
$ \mu{batch}^{k} $ ： 批标准化前，第k个卷积核， batch张输出特征图中所有像素点平均值
$ \sigma_{batch}^{k} $ ： 批标准化前，第k个卷积核， batch张输出特征图中所有像素点标准差

批标准化操作，会让每个像素点进行减均值除以标准差的自更新计算，对于 第k个卷积核batch张输出特征图中所有像素点平均值和标准差，是对 第k个卷积核产生的batch张输出特征图 集体求均值和标准差。

其中 $ \mu{batch}^{k} $ 和 $ \sigma{batch}^{k} $ 就是对第k个卷积核计算出来的batch张输出特征图中的所有像素点求均值和标准差。

BN操作将原本偏移的特征数据重新拉回到0均值，使进入激活函数的数据分布在激活函数线性区，使得输入数据的微小变化更明显体现到激活函数的输出，提升了激活函数对输入数据的区分力。

但是这种简单的特征数据标准化，使特征数据完全满足标准正态分布，集中在激活函数中心的线性区域，使激活函数丧失了非线性特性，因此在BN操作中为每个卷积核引入了两个可训练参数。缩放因子γ和偏移因子β。

反向传播时，缩放因子γ和偏移因子β会与其他待训练参数一同被训练优化，使标准正态分布后的特征数据通过缩放因子γ和偏移因子β优化了特征数据分布的宽窄和偏移量，保证了网络的非线性表达力。

BN层位于卷积层之后，激活层之前。

BN操作函数

tf.keras.layers.BatchNormalization()

model = tf.keras.models.Sequential([
    Conv2D(filters=6, kernel_size=(5, 5), padding='same'), # 卷积层
    BatchNormalization(), # BN层
    Activation('relu'), # 激活层
    MaxPool2D(pool_size=(2, 2), strides=2, padding='same'), # 池化层
    Dropout(0.2), # dropout层	
])

池化(Pooling)

池化操作作用于减少卷积神经网络中特征数据量（降维）。

池化的方法有最大池化和均值池化。
最大值池化可提取图片纹理，均值池化可保留背景特征。

如果用2×2的池化核对输入图片以2为步长进行池化，输出图片将变为输入图片的四分之一大小。

最大池化是用2×2的池化核框住左上4个像素点，选择最大的6输出。步长为2滑动到右上，选择最大的8输出，依次遍历图片。
均值池化和最大池化类似，提取的是4个像素点的均值，得到输出图片。

TF描述池化

tf.keras.layers.MaxPool2D(
    pool_size = 池化核尺寸,	#正方形写核长整数，或（核高h，核宽w）
    strides = 池化步长,	#步长整数， 或(纵向步长h，横向步长w)，默认为pool_size
    padding = 'valid' or 'same'	#使用全零填充是“same”， 不使用是“valid”（默认）
)

tf.keras.layers.AveragePooling2D(
    pool_size = 池化核尺寸,	#正方形写核长整数，或（核高h，核宽w）
    strides = 池化步长,	#步长整数， 或(纵向步长h，横向步长w)，默认为pool_size
    padding = 'valid' or 'same' #使用全零填充是“same”， 不使用是“valid”（默认）
)

model = tf.keras.models.Sequential([
    Conv2D(filters = 6, kernel_size = (5, 5), padding = 'same'), # 卷积层
    BatchNormalization(), # BN层
    Activation('relu'), # 激活层
    MaxPool2D(pool_size = (2, 2), strides = 2, padding = 'same'), # 池化层
    Dropout(0.2), # dropout层
])

舍弃(Dropout)

为了缓解神经网络过拟合，在神经网络训练过程中，常将隐藏层的部分神经元按照一定比例从神经网络中临时舍弃。在使用神经网络时，再把所有神经元恢复到神经网络中。

tf.keras.layers.Dropout(舍弃的概率)

model = tf.keras.models.Sequential([
    Conv2D(filters=6, kernel_size=(5, 5), padding='same'), # 卷积层
    BatchNormalization(), # BN层
    Activation('relu'), # 激活层
    MaxPool2D(pool_size=(2, 2), strides=2, padding='same'), # 池化层
    Dropout(0.2), # dropout层,随机舍弃掉20%神经元
])

卷积神经网络

卷积神经网络：借助卷积核提取特征后，送入全连接网络。

卷积是什么？ 卷积就是特征提取器，就是CBAPD

model = tf.keras.models.Sequential([
C	Conv2D(filters=6, kernel_size=(5, 5), padding='same'), # 卷积层
B	BatchNormalization(), # BN层
A	Activation('relu'), # 激活层
P	MaxPool2D(pool_size=(2, 2), strides=2, padding='same'), # 池化层
D	Dropout(0.2), # dropout层
])

cifar10数据集

提供 5万张 32 32 像素点的十分类彩色图片和标签，用于训练。
提供 1万张 32 32 像素点的十分类彩色图片和标签，用于测试。

import tensorflow as tf
from matplotlib import pyplot as plt
import numpy as np

np.set_printoptions(threshold=np.inf)

# 导入cifar10数据集
cifar10 = tf.keras.datasets.cifar10
(x_train, y_train), (x_test, y_test) = cifar10.load_data()

# 可视化训练集输入特征的第一个元素
plt.imshow(x_train[0])  # 绘制图片
plt.show()

# 打印出训练集输入特征的第一个元素
print("x_train[0]:\n", x_train[0])
# 打印出训练集标签的第一个元素
print("y_train[0]:\n", y_train[0])

# 打印出整个训练集输入特征形状
print("x_train.shape:\n", x_train.shape)
# 打印出整个训练集标签的形状
print("y_train.shape:\n", y_train.shape)
# 打印出整个测试集输入特征的形状
print("x_test.shape:\n", x_test.shape)
# 打印出整个测试集标签的形状
print("y_test.shape:\n", y_test.shape)

 [[177 144 116]
  [168 129  94]
  [179 142  87]
  [188 149  67]
  [202 168  68]
  [218 189  76]
  [218 191  72]
  [207 181  70]
  [191 163  79]
  [175 143  82]
  [166 132  86]
  [163 128  92]
  [163 127  94]
  [161 123  92]
  [153 114  84]
  [159 120  90]
  [162 124  93]
  [149 116  91]
  [140 104  83]
  [148 103  77]
  [161 105  69]
  [144  95  55]
  [112  90  59]
  [119  91  58]
  [130  96  65]
  [120  87  59]
  [ 92  67  46]
  [103  78  57]
  [170 140 104]
  [216 184 140]
  [151 118  84]
  [123  92  72]]]
y_train[0]:
 [6]
x_train.shape:
 (50000, 32, 32, 3)
y_train.shape:
 (50000, 1)
x_test.shape:
 (10000, 32, 32, 3)
y_test.shape:
 (10000, 1)

卷积神经网络搭建示例

import tensorflow as tf
import os
import numpy as np
from matplotlib import pyplot as plt
from tensorflow.keras.layers import Conv2D, BatchNormalization, Activation, MaxPool2D, Dropout, Flatten, Dense
from tensorflow.keras import Model

np.set_printoptions(threshold=np.inf)

cifar10 = tf.keras.datasets.cifar10
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0

#网络结构--start
######################################

class Baseline(Model):
    def __init__(self):
        super(Baseline, self).__init__()
        self.c1 = Conv2D(filters=6, kernel_size=(5, 5), padding='same')  # 卷积层
        self.b1 = BatchNormalization()  # BN层
        self.a1 = Activation('relu')  # 激活层
        self.p1 = MaxPool2D(pool_size=(2, 2), strides=2, padding='same')  # 池化层
        self.d1 = Dropout(0.2)  # dropout层

        self.flatten = Flatten()
        self.f1 = Dense(128, activation='relu')
        self.d2 = Dropout(0.2)
        self.f2 = Dense(10, activation='softmax')

    def call(self, x):
        x = self.c1(x)
        x = self.b1(x)
        x = self.a1(x)
        x = self.p1(x)
        x = self.d1(x)

        x = self.flatten(x)
        x = self.f1(x)
        x = self.d2(x)
        y = self.f2(x)
        return y

model = Baseline()

#网络结构--end
######################################

model.compile(optimizer='adam', loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False), metrics=['sparse_categorical_accuracy'])

checkpoint_save_path = "./checkpoint/Baseline.ckpt"
if os.path.exists(checkpoint_save_path + '.index'):
    print('-------------load the model-----------------')
    model.load_weights(checkpoint_save_path)

cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_save_path, save_weights_only=True, save_best_only=True)

history = model.fit(x_train, y_train, batch_size=32, epochs=5, validation_data=(x_test, y_test), validation_freq=1,  callbacks=[cp_callback])

model.summary()

# print(model.trainable_variables)
file = open('./weights.txt', 'w')
for v in model.trainable_variables:
    file.write(str(v.name) + '\n')
    file.write(str(v.shape) + '\n')
    file.write(str(v.numpy()) + '\n')
file.close()

###############################################    show   ###############################################

# 显示训练集和验证集的acc和loss曲线
acc = history.history['sparse_categorical_accuracy']
val_acc = history.history['val_sparse_categorical_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']

plt.subplot(1, 2, 1)
plt.plot(acc, label='Training Accuracy')
plt.plot(val_acc, label='Validation Accuracy')
plt.title('Training and Validation Accuracy')
plt.legend()

plt.subplot(1, 2, 2)
plt.plot(loss, label='Training Loss')
plt.plot(val_loss, label='Validation Loss')
plt.title('Training and Validation Loss')
plt.legend()
plt.show()

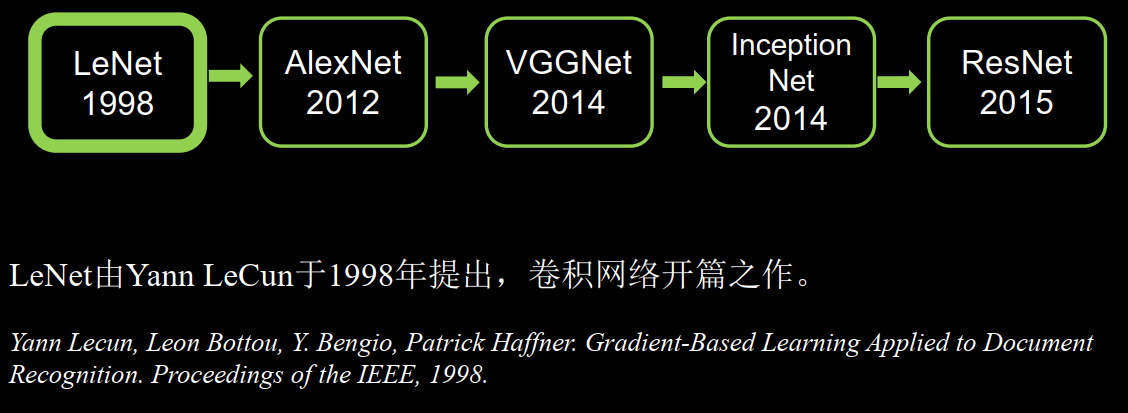
LeNet

LeCun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition.Proceedings of the IEEE, 1998, 86(11): 2278-2324.

通过共享卷积核减少了网络参数。

输入： 32323
C1卷积
C（核： 655，步长： 1，填充： valid ）
B（ None）
A（ sigmoid）
P（ max，核： 2*2，步长： 2，填充： valid ）
D（ None）

C3卷积
C（核： 1655，步长： 1，填充： valid ）
B（ None）
A（ sigmoid）
P（ max，核： 2*2，步长： 2，填充： valid ）
D（ None）

Flatten
Dense（神经元： 120，激活： sigmoid）
Dense（神经元： 84，激活： sigmoid）
Dense（神经元： 10，激活： softmax）

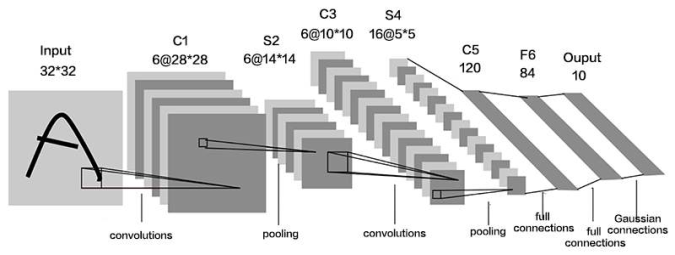
统计卷积神经网络层数时，一般只统计卷积计算层和全连接计算层，其余操作可以认为是卷积计算层的附属。

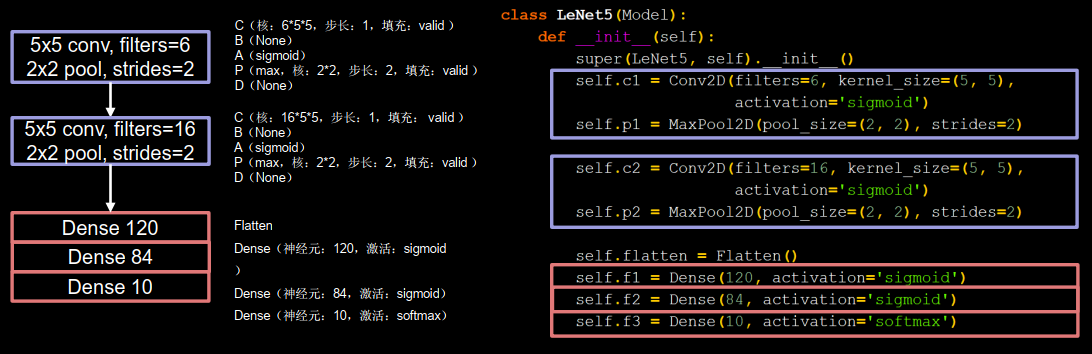
LeNet一共有五层网络

class LeNet5(Model):
    def __init__(self):
        super(LeNet5, self).__init__()
        self.c1 = Conv2D(filters=6, kernel_size=(5, 5), activation='sigmoid')
        self.p1 = MaxPool2D(pool_size=(2, 2), strides=2)

        self.c2 = Conv2D(filters=16, kernel_size=(5, 5), activation='sigmoid')
        self.p2 = MaxPool2D(pool_size=(2, 2), strides=2)

        self.flatten = Flatten()
        self.f1 = Dense(120, activation='sigmoid')
        self.f2 = Dense(84, activation='sigmoid')
        self.f3 = Dense(10, activation='softmax')

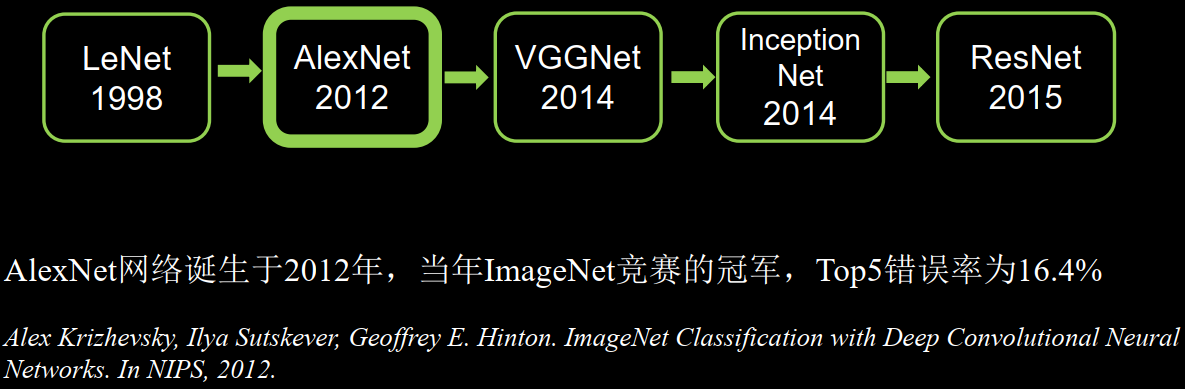
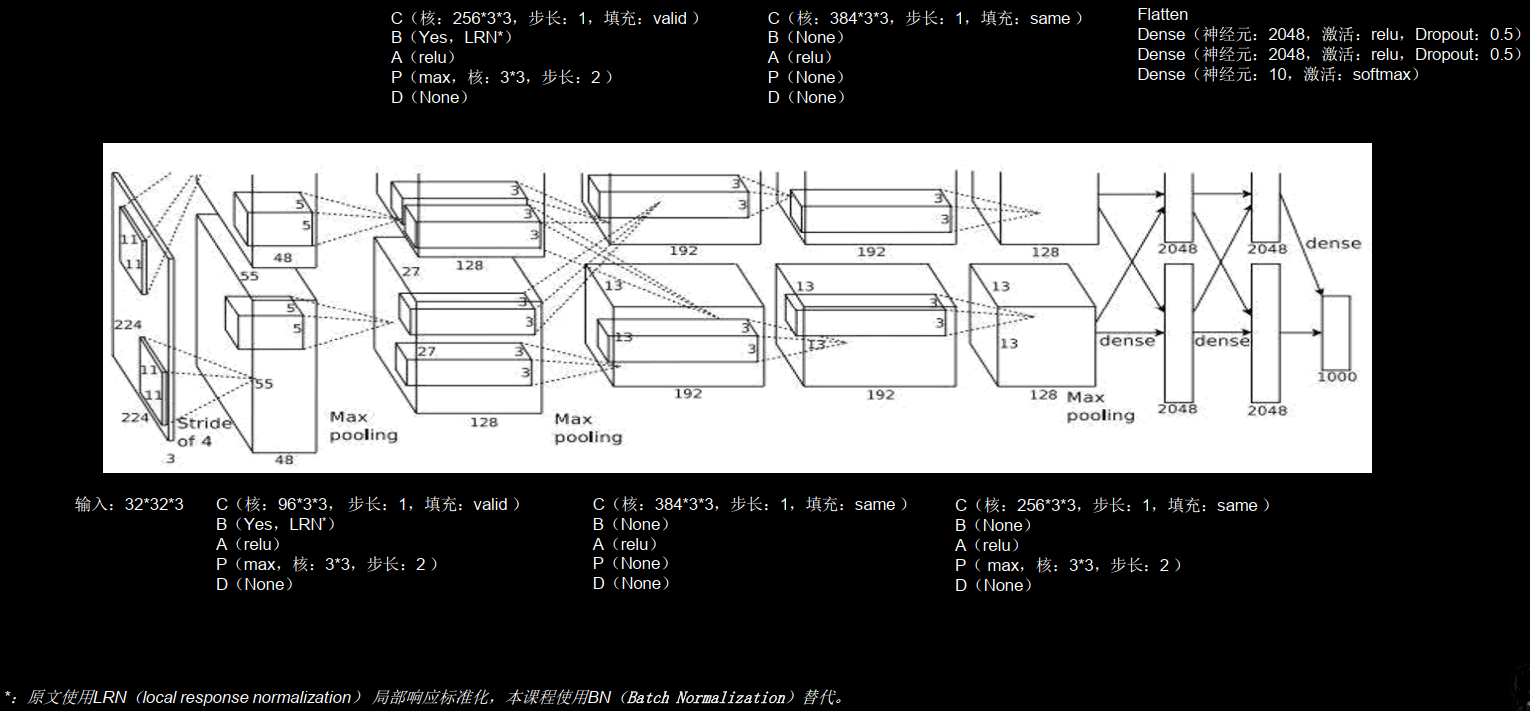
AlexNet

Alex Krizhevsky, Ilya Sutskever, Geoffrey E. Hinton. ImageNet Classification with Deep Convolutional NeuralNetworks. In NIPS, 2012.

使用relu激活函数提升激活速度，使用了dropout缓解了过拟合，

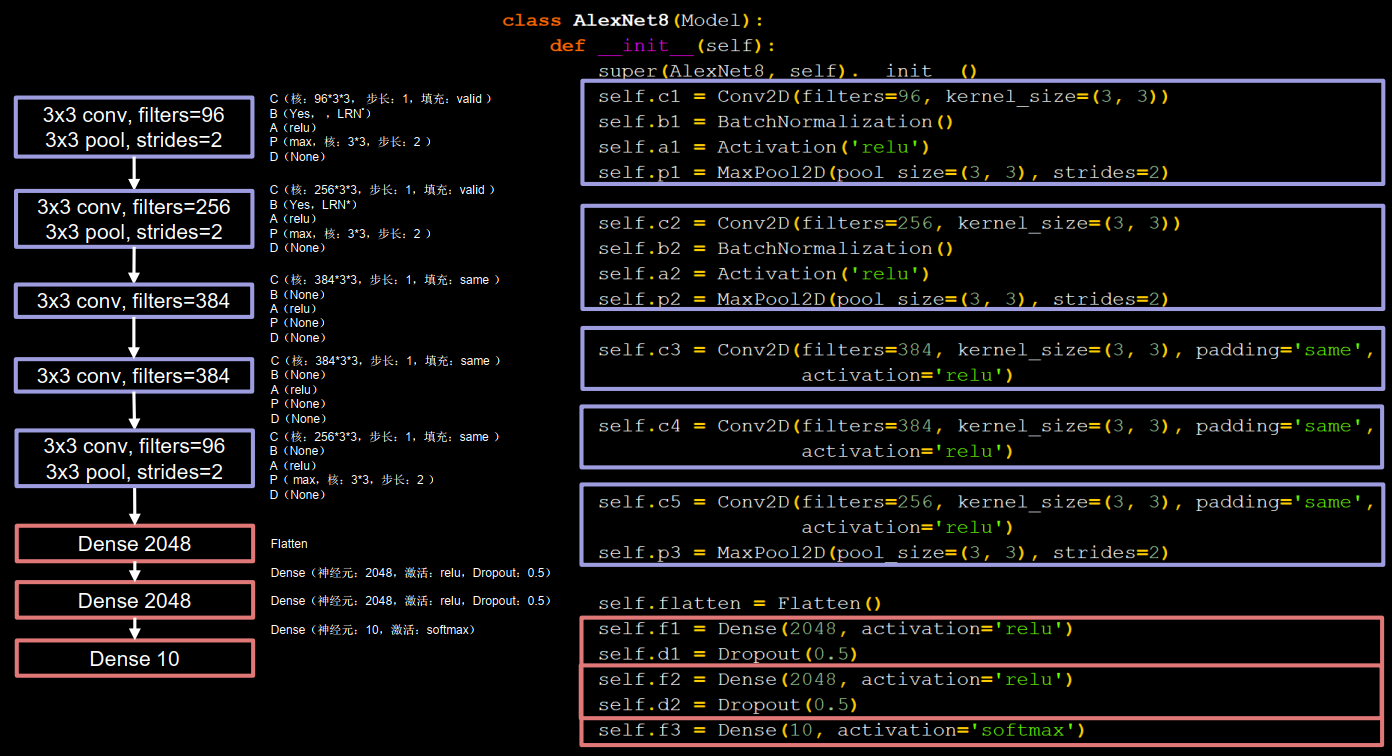
class AlexNet8(Model):
    def __init__(self):
        super(AlexNet8, self).__init__()
        self.c1 = Conv2D(filters=96, kernel_size=(3, 3))
        self.b1 = BatchNormalization()
        self.a1 = Activation('relu')
        self.p1 = MaxPool2D(pool_size=(3, 3), strides=2)

        self.c2 = Conv2D(filters=256, kernel_size=(3, 3))
        self.b2 = BatchNormalization()
        self.a2 = Activation('relu')
        self.p2 = MaxPool2D(pool_size=(3, 3), strides=2)

        self.c3 = Conv2D(filters=384, kernel_size=(3, 3), padding='same', activation='relu')
                         
        self.c4 = Conv2D(filters=384, kernel_size=(3, 3), padding='same', activation='relu')
                         
        self.c5 = Conv2D(filters=256, kernel_size=(3, 3), padding='same', activation='relu')        
        self.p3 = MaxPool2D(pool_size=(3, 3), strides=2)

        self.flatten = Flatten()
        self.f1 = Dense(2048, activation='relu')
        self.d1 = Dropout(0.5)
        self.f2 = Dense(2048, activation='relu')
        self.d2 = Dropout(0.5)
        self.f3 = Dense(10, activation='softmax')

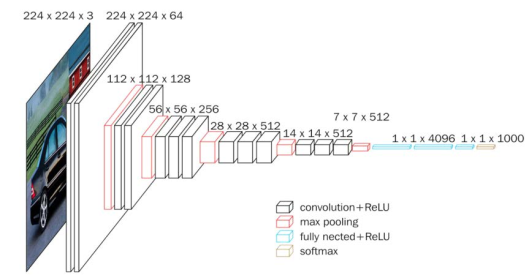
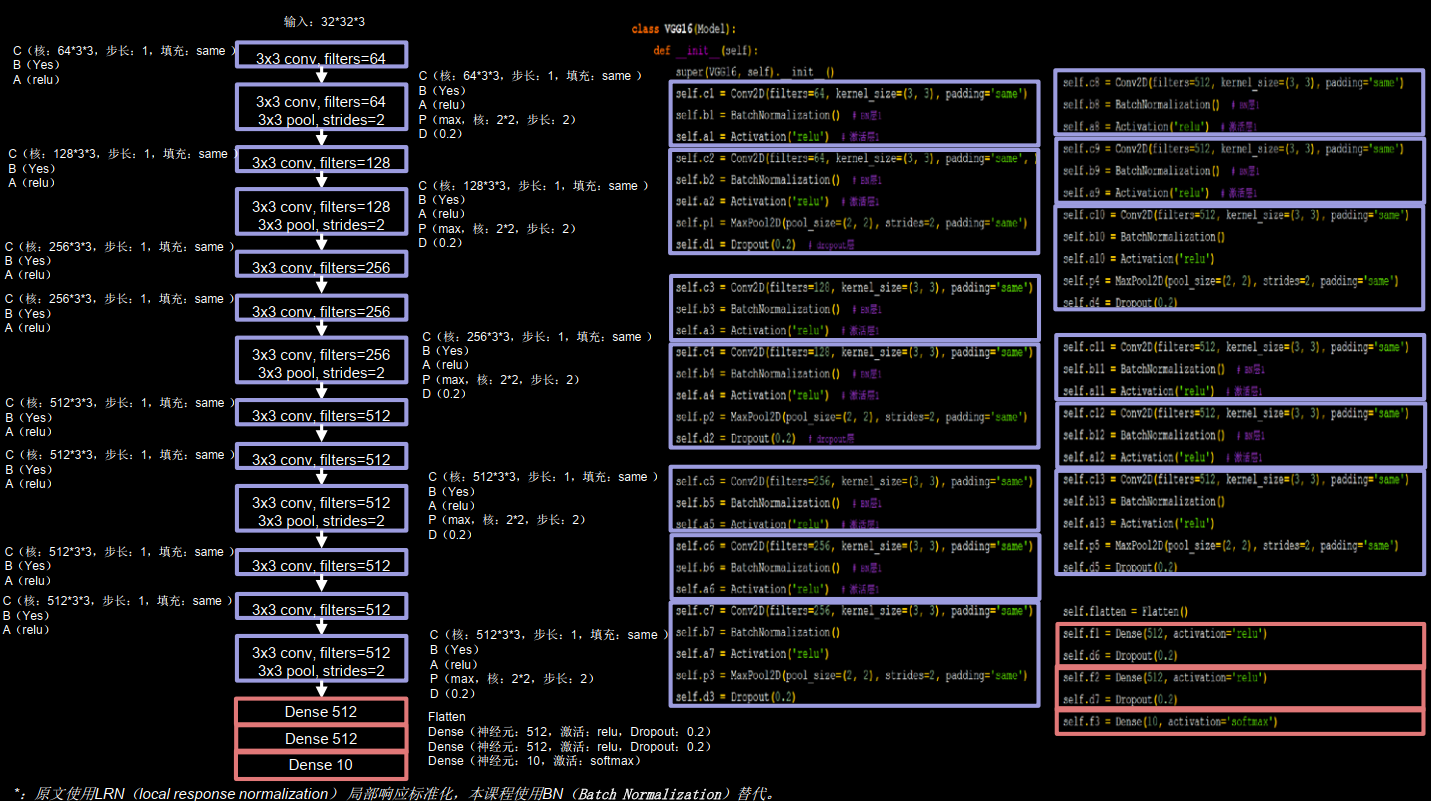
VGGNet

K. Simonyan, A. Zisserman. Very Deep Convolutional Networks for Large-Scale Image Recognition.In ICLR,2015

适合硬件加速

16层VGG网络

class VGG16(Model):
    def __init__(self):
        super(VGG16, self).__init__()
        # A） 第一部分： 两次卷积（64 个 3 * 3 卷积核、 BN、 Relu 激活） →最大池化→Dropout
        self.c1 = Conv2D(filters=64, kernel_size=(3, 3), padding='same')  # 卷积层1
        self.b1 = BatchNormalization()  # BN层1
        self.a1 = Activation('relu')  # 激活层1
        
        self.c2 = Conv2D(filters=64, kernel_size=(3, 3), padding='same', )
        self.b2 = BatchNormalization()  # BN层1
        self.a2 = Activation('relu')  # 激活层1
        self.p1 = MaxPool2D(pool_size=(2, 2), strides=2, padding='same')
        self.d1 = Dropout(0.2)  # dropout层

        # B） 第二部分： 两次卷积（128 个 3 * 3 卷积核、 BN、 Relu 激活） →最大池化→Dropout
        self.c3 = Conv2D(filters=128, kernel_size=(3, 3), padding='same')
        self.b3 = BatchNormalization()  # BN层1
        self.a3 = Activation('relu')  # 激活层1
        
        self.c4 = Conv2D(filters=128, kernel_size=(3, 3), padding='same')
        self.b4 = BatchNormalization()  # BN层1
        self.a4 = Activation('relu')  # 激活层1
        self.p2 = MaxPool2D(pool_size=(2, 2), strides=2, padding='same')
        self.d2 = Dropout(0.2)  # dropout层

        # C） 第三部分： 三次卷积（256 个 3 * 3 卷积核、 BN、 Relu 激活） →最大池化→Dropout
        self.c5 = Conv2D(filters=256, kernel_size=(3, 3), padding='same')
        self.b5 = BatchNormalization()  # BN层1
        self.a5 = Activation('relu')  # 激活层1
        
        self.c6 = Conv2D(filters=256, kernel_size=(3, 3), padding='same')
        self.b6 = BatchNormalization()  # BN层1
        self.a6 = Activation('relu')  # 激活层1
        
        self.c7 = Conv2D(filters=256, kernel_size=(3, 3), padding='same')
        self.b7 = BatchNormalization()
        self.a7 = Activation('relu')
        self.p3 = MaxPool2D(pool_size=(2, 2), strides=2, padding='same')
        self.d3 = Dropout(0.2)

        # D） 第四部分： 三次卷积（512 个 3 * 3 卷积核、 BN、 Relu 激活） →最大池化→Dropout
        self.c8 = Conv2D(filters=512, kernel_size=(3, 3), padding='same')
        self.b8 = BatchNormalization()  # BN层1
        self.a8 = Activation('relu')  # 激活层1
        
        self.c9 = Conv2D(filters=512, kernel_size=(3, 3), padding='same')
        self.b9 = BatchNormalization()  # BN层1
        self.a9 = Activation('relu')  # 激活层1
        
        self.c10 = Conv2D(filters=512, kernel_size=(3, 3), padding='same')
        self.b10 = BatchNormalization()
        self.a10 = Activation('relu')
        self.p4 = MaxPool2D(pool_size=(2, 2), strides=2, padding='same')
        self.d4 = Dropout(0.2)

        # E） 第五部分： 三次卷积（ 512 个 3 * 3 卷积核、 BN、 Relu 激活） →最大池化→Dropout
        self.c11 = Conv2D(filters=512, kernel_size=(3, 3), padding='same')
        self.b11 = BatchNormalization()  # BN层1
        self.a11 = Activation('relu')  # 激活层1
        
        self.c12 = Conv2D(filters=512, kernel_size=(3, 3), padding='same')
        self.b12 = BatchNormalization()  # BN层1
        self.a12 = Activation('relu')  # 激活层1
        
        self.c13 = Conv2D(filters=512, kernel_size=(3, 3), padding='same')
        self.b13 = BatchNormalization()
        self.a13 = Activation('relu')
        self.p5 = MaxPool2D(pool_size=(2, 2), strides=2, padding='same')
        self.d5 = Dropout(0.2)

        # F） 第六部分： 全连接（ 512 个神经元） →Dropout→全连接（ 512 个神经元） →Dropout→全连接（ 10 个神经元）
        self.flatten = Flatten()
        self.f1 = Dense(512, activation='relu')
        self.d6 = Dropout(0.2)
        self.f2 = Dense(512, activation='relu')
        self.d7 = Dropout(0.2)
        self.f3 = Dense(10, activation='softmax')

卷积核的个数从64到128到256到512，逐渐增加，因为越靠后，特征图尺寸越小，通过增加卷积核的个数，增加了特征图深度，保持了信息的承载能力。

InceptionNet

Szegedy C, Liu W, Jia Y, et al. Going Deeper with Convolutions. In CVPR, 2015.

InceptionNet引入了Inception结构块，在同一层网络内使用不同尺寸的卷积核，提升了模型感知力，使用了批标准化，缓解了梯度消失。

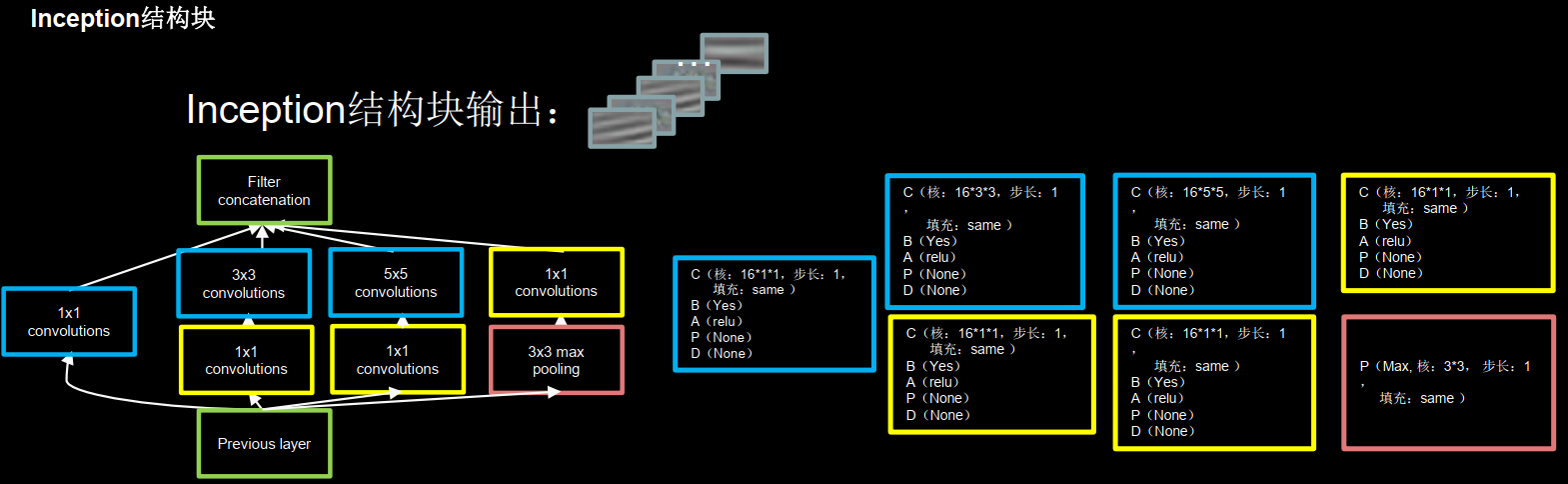
Inception结构块在同一层网络中使用了多个尺寸的卷积核，可以提取不同尺寸的特征，通过1 × 1卷积核，作用到输入特征图的每个像素点。通过设定少于输入特征图深度的1 × 1卷积核个数，减少了输出特征图深度，起到了降维的作用，减少了参数量和计算量。

一个Inception结构块包含四个分支，
分别经过 1 × 1 卷积核输出到卷积连接器，
经过 1 × 1 卷积核配合 3 × 3 卷积核输出到卷积连接器，
经过 1 × 1 卷积核配合 5 × 5 卷积核输出到卷积连接器，
经过 3 × 3 最大池化核配合 1 × 1 卷积核输出到卷积连接器。

送到卷积连接器的特征数据尺寸相同，卷积连接器会把收到的这四路特征数据按深度方向拼接，形成Inception结构块的输出。

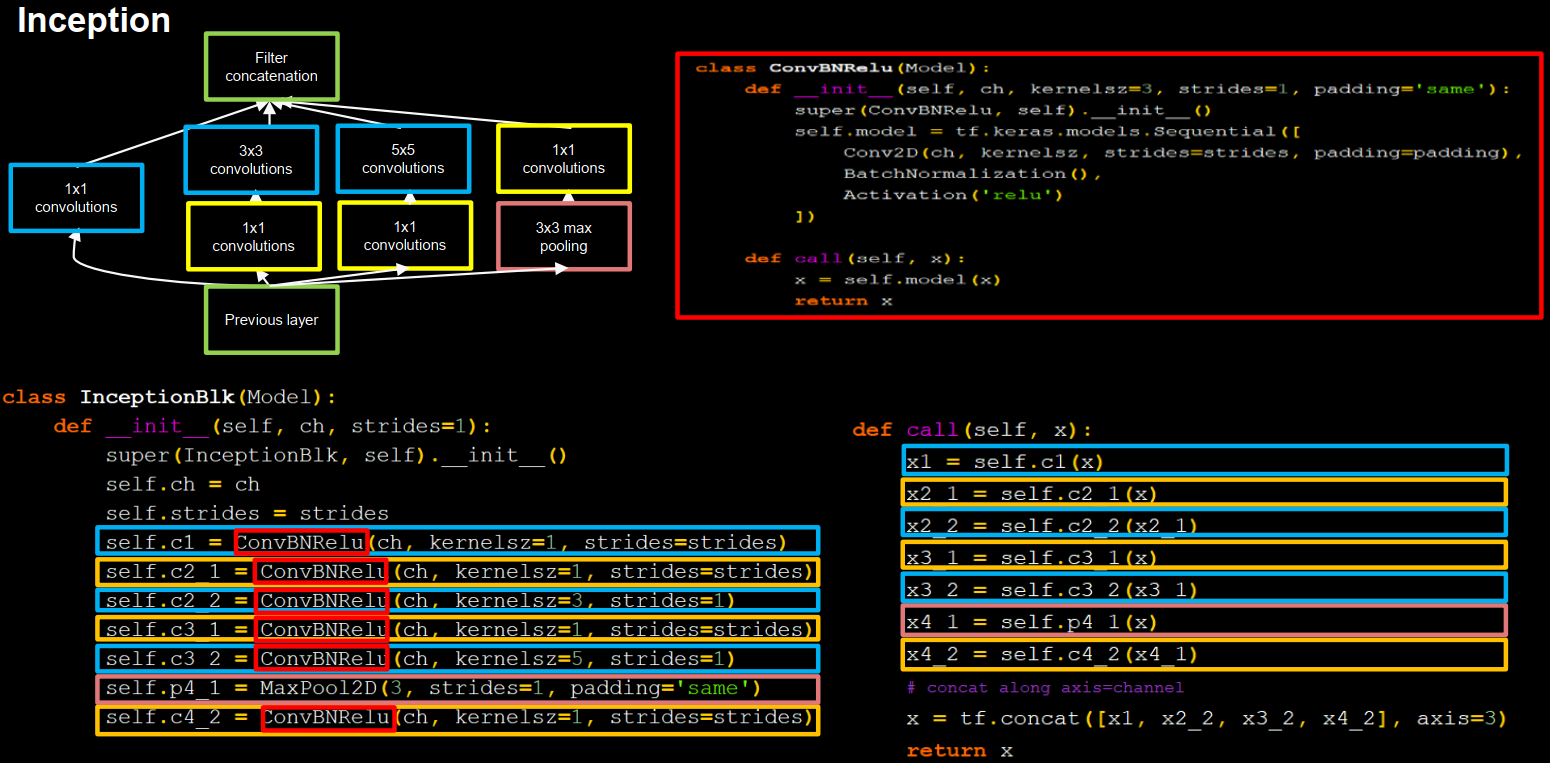
Inception结构块中的卷积操作均采用了CBA结构，先卷积，再BN，再采用relu激活函数，所以将其定义成一个新的类ConvBNRelu，可以减少代码长度。

class ConvBNRelu(Model):
    def __init__(self, ch, kernelsz=3, strides=1, padding='same'):
        super(ConvBNRelu, self).__init__()
        self.model = tf.keras.models.Sequential([
            Conv2D(ch, kernelsz, strides=strides, padding=padding),
            BatchNormalization(),
            Activation('relu')
        ])

    def call(self, x):
        x = self.model(x, training=False) #在training=False时，BN通过整个训练集计算均值、方差去做批归一化，training=True时，通过当前batch的均值、方差去做批归一化。推理时 training=False效果好
        return x

class InceptionBlk(Model):
    def __init__(self, ch, strides=1):
        super(InceptionBlk, self).__init__()
        self.ch = ch
        self.strides = strides
        self.c1 = ConvBNRelu(ch, kernelsz=1, strides=strides)
        self.c2_1 = ConvBNRelu(ch, kernelsz=1, strides=strides)
        self.c2_2 = ConvBNRelu(ch, kernelsz=3, strides=1)
        self.c3_1 = ConvBNRelu(ch, kernelsz=1, strides=strides)
        self.c3_2 = ConvBNRelu(ch, kernelsz=5, strides=1)
        self.p4_1 = MaxPool2D(3, strides=1, padding='same')
        self.c4_2 = ConvBNRelu(ch, kernelsz=1, strides=strides)

    def call(self, x):
        x1 = self.c1(x)
        x2_1 = self.c2_1(x)
        x2_2 = self.c2_2(x2_1)
        x3_1 = self.c3_1(x)
        x3_2 = self.c3_2(x3_1)
        x4_1 = self.p4_1(x)
        x4_2 = self.c4_2(x4_1)
        # concat along axis=channel
        x = tf.concat([x1, x2_2, x3_2, x4_2], axis=3)# 深度方向堆叠
        return x

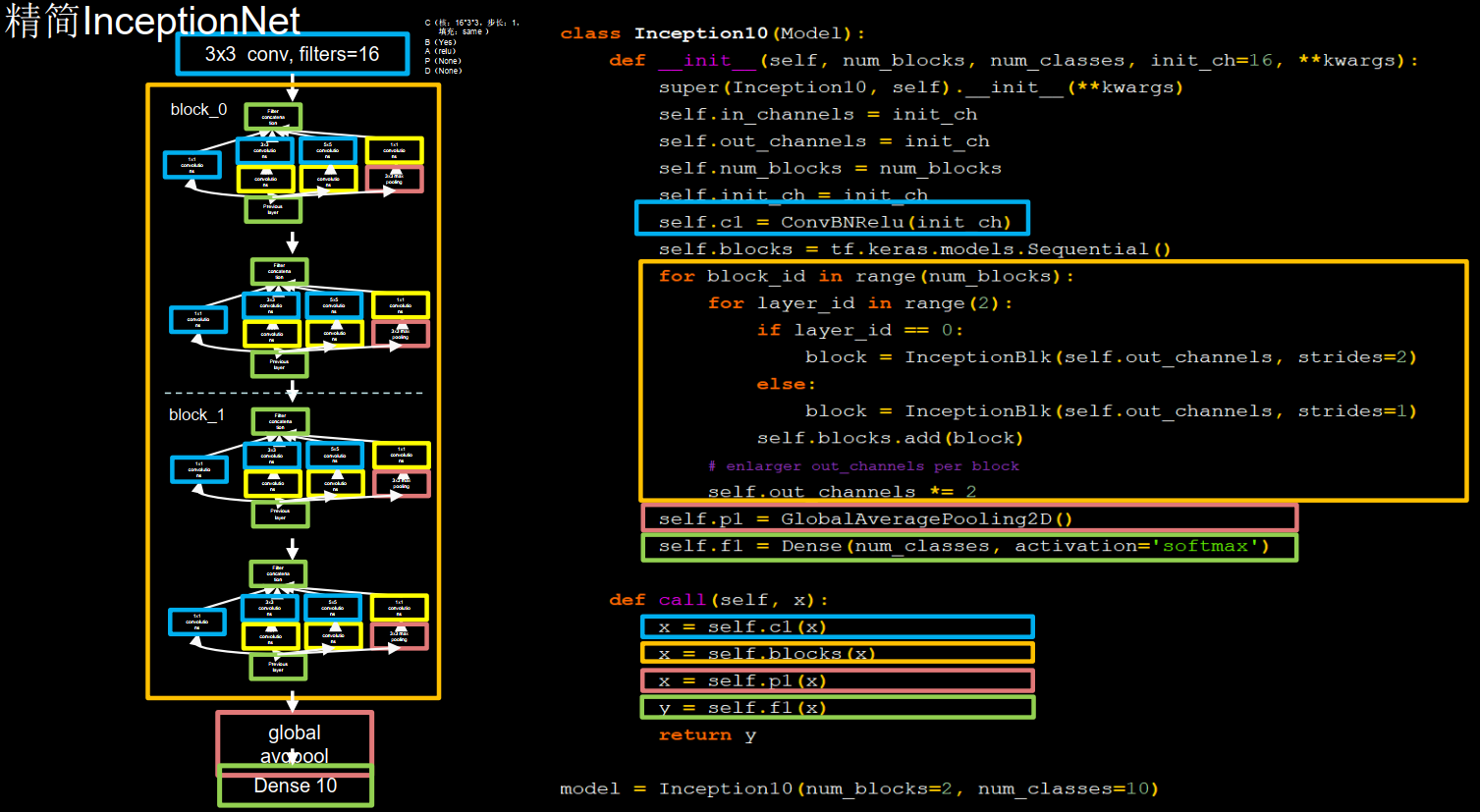
每两个inception结构块组合成一个block，每个block中第一个Inception结构块卷积步长是2，第二个Inception结构块卷积步长是1，这使得第一个Inception结构块输出特征图尺寸减半。因此将输出图特征图深度加深，尽可能保证特征抽取中信息的承载量一致，block_0 设置的通道数是16，经过了四个分支，输出的深度为 4 × 16 = 64。在这里给通道数加倍了，所以 block_1 通道数是 block_0 通道数的两倍，是32，同样，经过了四个分支，输出深度是 4 × 32 = 128。128个数据会被送进平均池化，送进十个分类的全连接，这里实例化了Inception10的类，指定了InceptionNet的block数是2，也就是 block_0 和 block_1 ，而后网络指定分几类。

class Inception10(Model):
    def __init__(self, num_blocks, num_classes, init_ch=16, **kwargs):
        super(Inception10, self).__init__(**kwargs)
        self.in_channels = init_ch
        self.out_channels = init_ch
        self.num_blocks = num_blocks
        self.init_ch = init_ch
        self.c1 = ConvBNRelu(init_ch)
        self.blocks = tf.keras.models.Sequential()
        for block_id in range(num_blocks):
            for layer_id in range(2):
                if layer_id == 0:
                    block = InceptionBlk(self.out_channels, strides=2)
                else:
                    block = InceptionBlk(self.out_channels, strides=1)
                self.blocks.add(block)
            # enlarger out_channels per block
            self.out_channels *= 2
        self.p1 = GlobalAveragePooling2D()
        self.f1 = Dense(num_classes, activation='softmax')

    def call(self, x):
        x = self.c1(x)
        x = self.blocks(x)
        x = self.p1(x)
        y = self.f1(x)
        return y


model = Inception10(num_blocks=2, num_classes=10)

训练时候可以调节batchsize大小，使显卡达到70%利用率即可。

ResNet

Kaiming He, Xiangyu Zhang, Shaoqing Ren. Deep Residual Learning for Image Recognition. In CPVR,2016

ResNet提出了层间残差跳连，引入前方信息，缓解梯度消失，使神经网络层数增加成为可能。

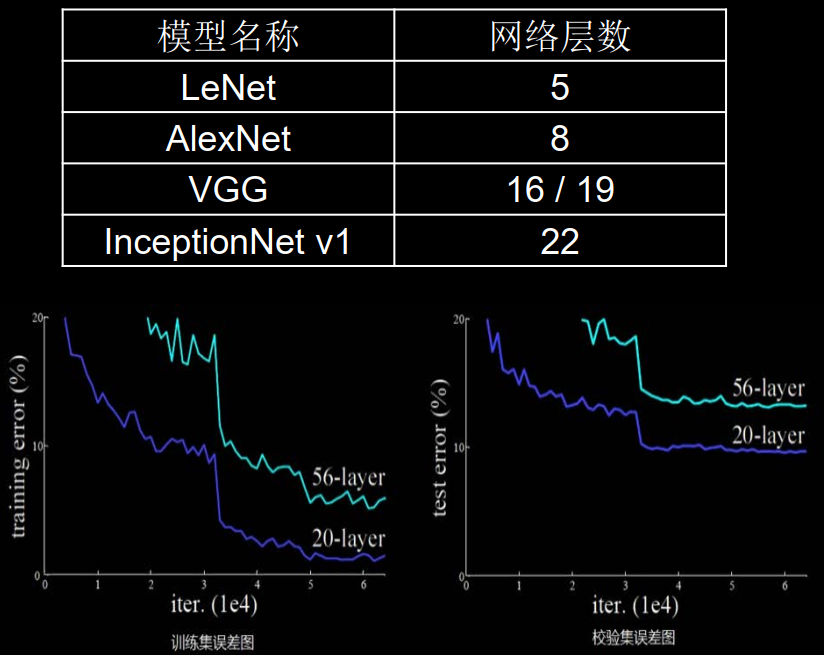
通过加深网络层数，取得了越来越好的效果。

然56层卷积网络错误率要高于20层卷积网络。

单纯的堆叠网络层数会使得网络模型退化，以至于后边特征丢失了前边特征的原本模样。

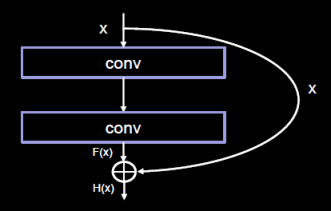
于是使用跳连线，将前边特征直接接到了后边，使得 H(x) 包含了堆叠卷积的非线性输出 F(x) ，和跳过这两层堆叠卷积，直接连接过来的恒等映射x，让它们的对应元素相加，这一操作有效缓解了神经网络模型堆叠导致的退化，使得神经网络可以向更深层级发展。

Inception块中的 “+” 是沿深度方向叠加（千层蛋糕层数叠加）
ResNet块中的 “+” 是特征图对应元素值相加（矩阵值相加）

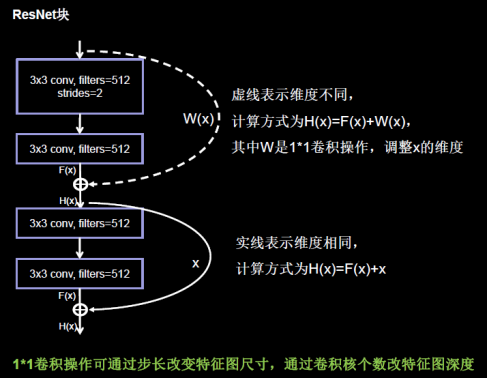
ResNet块中有两种情况，一种情况用图中的实线表示，这种情况两层堆叠卷积，没有改变特征图的维度，也就是它们特征图的个数、高、宽和深度都相同，可以直接将 F(x) 与 x 相加。
另一种情况用图中的虚线表示，这种情况中两层堆叠卷积改变了特征图的维度，需要借助 1 × 1 的卷积来调整 x 的维度，使 W(x) 与 F(x) 的维度一致。

ResNet块有两种形式，一种在堆叠卷积前后维度相同，另一种在堆叠卷积前后维度不同。
将ResNet块的两种结构封装到一个橙色块中，写出ResnetBlock类，每调用一次ResnetBlock类，会生成一个黄色块，如果堆叠卷积前后维度不同，residual_path 等于1，调用红色块里的代码，使用1 × 1卷积操作，调整输入特征图inputs的尺寸或深度后，将堆叠卷积输出特征 y 和 if 语句计算出的residual 相加，过激活，输出。
如果堆叠卷积前后维度相同，不执行红色块内的代码，直接将堆叠卷积输出特征y和输入特征图inputs相加，过激活，输出。
后续代码用橙色块拼接完成。

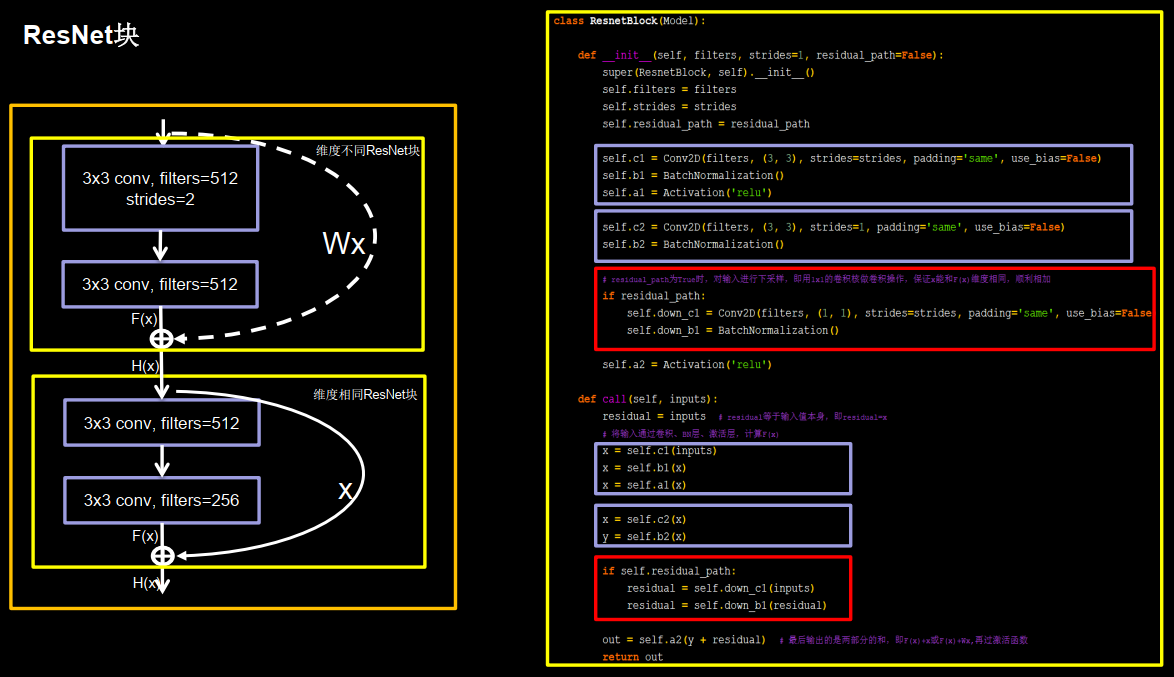
class ResnetBlock(Model):

    def __init__(self, filters, strides=1, residual_path=False):
        super(ResnetBlock, self).__init__()
        self.filters = filters
        self.strides = strides
        self.residual_path = residual_path

        self.c1 = Conv2D(filters, (3, 3), strides=strides, padding='same', use_bias=False)
        self.b1 = BatchNormalization()
        self.a1 = Activation('relu')

        self.c2 = Conv2D(filters, (3, 3), strides=1, padding='same', use_bias=False)
        self.b2 = BatchNormalization()

        # residual_path为True时，对输入进行下采样，即用1x1的卷积核做卷积操作，保证x能和F(x)维度相同，顺利相加
        if residual_path:
            self.down_c1 = Conv2D(filters, (1, 1), strides=strides, padding='same', use_bias=False)
            self.down_b1 = BatchNormalization()
        
        self.a2 = Activation('relu')

    def call(self, inputs):
        residual = inputs  # residual等于输入值本身，即residual=x
        # 将输入通过卷积、BN层、激活层，计算F(x)
        x = self.c1(inputs)
        x = self.b1(x)
        x = self.a1(x)

        x = self.c2(x)
        y = self.b2(x)

        if self.residual_path:
            residual = self.down_c1(inputs)
            residual = self.down_b1(residual)

        out = self.a2(y + residual)  # 最后输出的是两部分的和，即F(x)+x或F(x)+Wx,再过激活函数
        return out

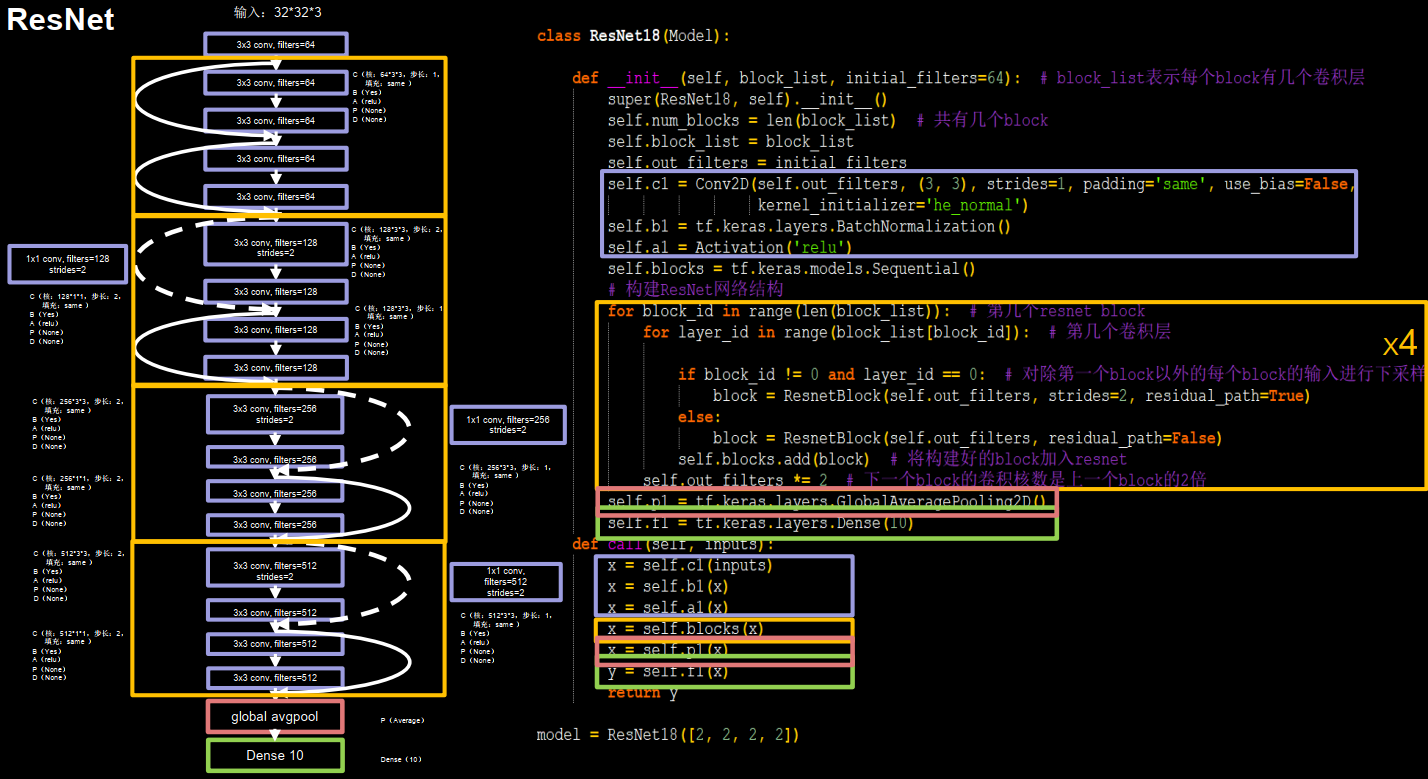
左侧给出的框图是ResNet18用CBAPD表示的结构，

class ResNet18(Model):

    def __init__(self, block_list, initial_filters=64):  # block_list表示每个block有几个卷积层
        super(ResNet18, self).__init__()
        self.num_blocks = len(block_list)  # 共有几个block
        self.block_list = block_list
        self.out_filters = initial_filters
        self.c1 = Conv2D(self.out_filters, (3, 3), strides=1, padding='same', use_bias=False)
        self.b1 = BatchNormalization()
        self.a1 = Activation('relu')
        self.blocks = tf.keras.models.Sequential()
        # 构建ResNet网络结构
        for block_id in range(len(block_list)):  # 第几个resnet block
            for layer_id in range(block_list[block_id]):  # 第几个卷积层

                if block_id != 0 and layer_id == 0:  # 对除第一个block以外的每个block的输入进行下采样
                    block = ResnetBlock(self.out_filters, strides=2, residual_path=True)
                else:
                    block = ResnetBlock(self.out_filters, residual_path=False)
                self.blocks.add(block)  # 将构建好的block加入resnet
            self.out_filters *= 2  # 下一个block的卷积核数是上一个block的2倍
        self.p1 = tf.keras.layers.GlobalAveragePooling2D()
        self.f1 = tf.keras.layers.Dense(10, activation='softmax', kernel_regularizer=tf.keras.regularizers.l2())

    def call(self, inputs):
        x = self.c1(inputs)
        x = self.b1(x)
        x = self.a1(x)
        x = self.blocks(x)
        x = self.p1(x)
        y = self.f1(x)
        return y

model = ResNet18([2, 2, 2, 2])

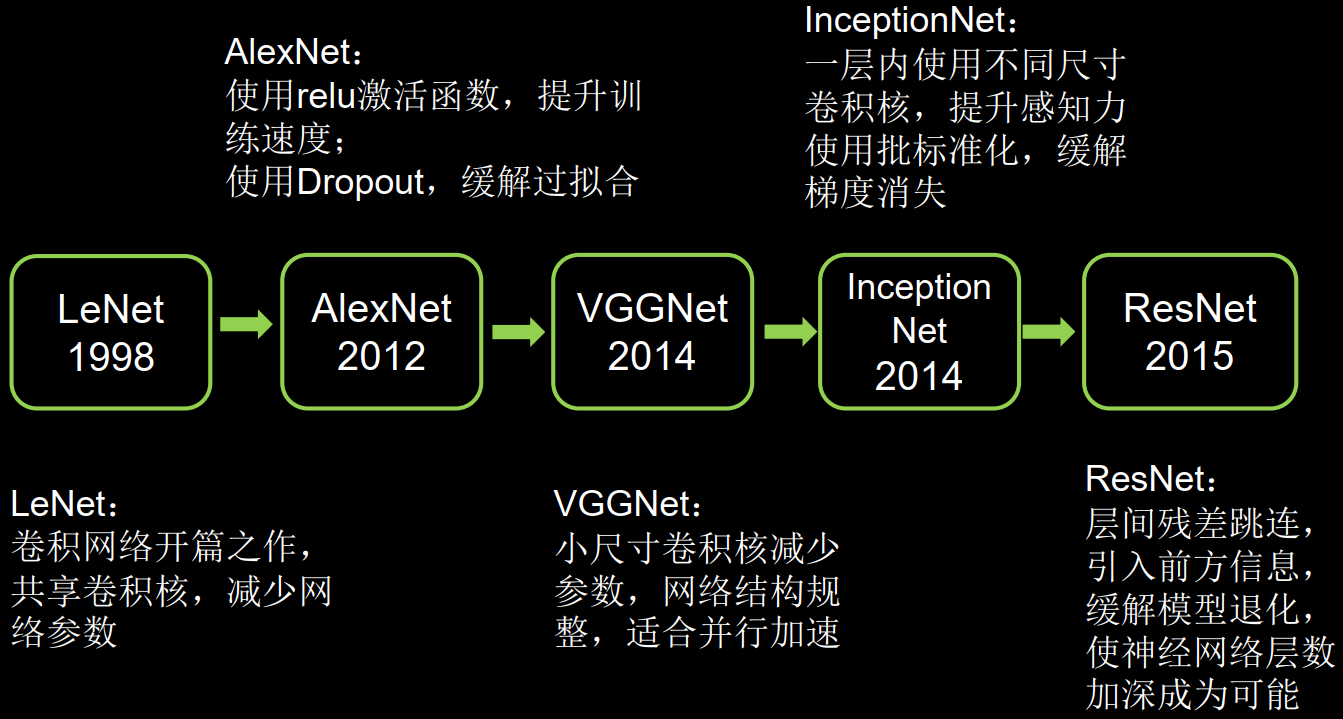
经典卷积及网络小结