HibisciDai 主页关于我归档标签分类相册
人工智能实践-Tensorflow笔记-MOOC-第二讲神经网络优化
|学习笔记
字数总计: 20.7k|阅读时长: 90 分钟

人工智能实践-Tensorflow笔记-MOOC-第二讲神经网络优化

[TOC]

人工智能实践-Tensorflow笔记-MOOC-第二讲神经网络优化

预备知识

tf.where() | 判断

  • 条件语句真返回A，条件语句假返回B
1
tf.where(条件语句, 真返回A, 假返回B)
1
2
3
4
a=tf.constant([1, 2, 3, 1, 1])
b=tf.constant([0, 1, 3, 4, 5])
c=tf.where(tf.greater(a, b), a, b) # 若a>b,返回a对应位置的元素，否则返回b对应位置的元素
print("c:", c)

运行结果：

1
c: tf.Tensor([1 2 3 4 5], shape=(5,), dtype=int32)

np.random.RandomState.rand() | 随机数

  • 返回一个[0, 1)之间的随机数
1
np.random.RandomState.rand(维度)	#维度为空，返回标量
1
2
3
4
5
6
import numpy as np
rdm = np.random.RandomState(seed = 1) # seed=常数每次生成随机数相同
a = rdm.rand() # 返回一个随机标量
b = rdm.rand(2, 3) # 返回维度为2行3列随机数矩阵
print("a:", a)
print("b:", b)

运行结果：

1
2
3
a: 0.417022004702574
b: [[7.20324493e-01 1.14374817e-04 3.02332573e-01]
	[1.46755891e-01 9.23385948e-02 1.86260211e-01]]

np.vstack() | 拼接叠加

  • 将两个数组按垂直方向叠加
1
np.vstack(数组1, 数组2)
1
2
3
4
5
import numpy as np
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
c = np.vstack((a, b))
print("c:\n", c)

运行结果：

1
2
3
c:
[[1 2 3]
[4 5 6]]

np.mgrid .ravel .c | 网格坐标点

通常配合使用，可以生成网格坐标点

np.mgrid

  • 返回若干组纬度相同的等差数组
1
2
np.mgrid[起始值 : 结束值 : 步长 , 起始值 : 结束值 : 步长 , … ]
# [起始值, 结束值)

x.ravel()

  • 将x变为一维数组

相当于把变量拉直

np.c

  • 使返回的间隔数值点配对
1
np.c_[数组1, 数组2, ...]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import numpy as np
x, y = np.mgrid [1:3:1, 2:4:0.5]
# 第一个等差数组返回 1., 2.
# 第二个等差数组返回 2., 2.5, 3., 3.5
# 为了保证纬度相同, 以数多的为准, 所以返回两行四列

grid = np.c_[x.ravel(), y.ravel()]
# 讲x和y配对输出
# x = 1. 时
# y = 2., 2.5, 3., 3.5
# [1. 2.] [1. 2.5] [1. 3.] [1. 3.5]
# x = 2. 时
# y = 2., 2.5, 3., 3.5
# [2. 2.] [2. 2.5] [2. 3.] [2. 3.5]

print("x:", x)
print("y:", y)
print('grid:\n', grid)

运行结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
x = [[1. 1. 1. 1.]
	[2. 2. 2. 2.]]
y = [[2. 2.5 3. 3.5]
	[2. 2.5 3. 3.5]]

grid:
[[1. 2. ]
[1. 2.5]
[1. 3. ]
[1. 3.5]
[2. 2. ]
[2. 2.5]
[2. 3. ]
[2. 3.5]]

复杂度学习率

空间复杂度用神经网络层数和神经网络中待优化参数的个数表示

时间复杂度可以用神经网络中乘加运算的次数表示

计算神经网络层数时，只统计具有运算能力的层

输入层仅仅把数据传输过来，没有运算，统计网络层数时候，不算输入层

输入层和输出层之间，所有层都叫做隐藏层

神经网络的层数是n个隐藏层的层数加上1个输出层

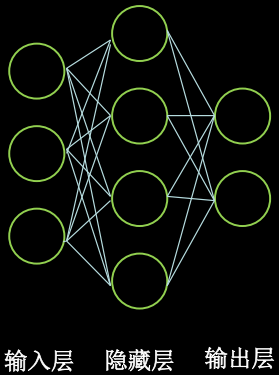
时间空间复杂度

输入层有三个节点

隐藏层只有一层，有四个节点

输出层有两个节点

这个网络共有两层神经网络，分别是隐藏层和输出层

参数的个数是所有w和b的总数

第一层参数是三行四列个w加上4个偏置项b，每个神经元有一个偏置项b，有3 * 4 + 4 = 16 个参数

第二层参数是四行两列个w加上2个偏置项b，每个神经元有一个偏置项b，有4 * 2 + 2 = 10 个参数

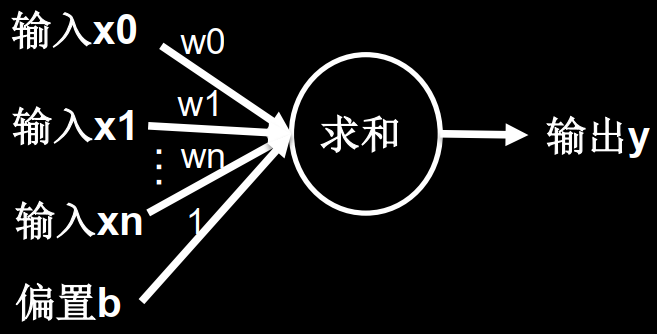
每个具有计算能力的神经元小球，都要收集前一层的每一个输入特征乘以各自线上的权重w，再加上这个神经元的偏置项b。

空间复杂度分析

层数 = 隐藏层的层数 + 1个输出层 = 2

总参数 = 总w + 总b = 26
第一层 = 3×4+4 = 16
第二层 = 4×2+2 = 10

时间复杂度分析

乘加运算次数 = 20
第一层 = 3×4 = 12
第二层 = 4×2 = 8

学习率

$ w_{t+1} $ : 更新后的参数

$ w_{t} $ : 当前参数

$ lr $ : 学习率

$ \frac{\partial loss}{\partial w_{t}} $ ：损失函数的梯度（偏导数）

损失函数：

$ \frac{\partial loss}{\partial w_{t}} = 2w+2 $

参数w初始化为5，学习率为0.2，则
1次 参数w=5 5-0.2×(2×5+2)=2.6
2次 参数w=2.6 2.6-0.2×(2×2.6+2)=1.16
3次 参数w=1.16 1.16-0.2×(2×1.16+2)=0.296
4次 参数w=0.296
…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import tensorflow as tf

w = tf.Variable(tf.constant(5, dtype=tf.float32))
lr = 0.2
epoch = 40

for epoch in range(epoch):  # for epoch 定义顶层循环，表示对数据集循环epoch次，此例数据集数据仅有1个w,初始化时候constant赋值为5，循环40次迭代。
    with tf.GradientTape() as tape:  # with结构到grads框起了梯度的计算过程。
        loss = tf.square(w + 1)
    grads = tape.gradient(loss, w)  # .gradient函数告知谁对谁求导

    w.assign_sub(lr * grads)  # .assign_sub 对变量做自减 即：w -= lr*grads 即 w = w - lr*grads
    print("After %s epoch,w is %f,loss is %f" % (epoch, w.numpy(), loss))

# lr初始值：0.2   请自改学习率  0.001  0.999 看收敛过程
# 最终目的：找到 loss 最小 即 w = -1 的最优参数w

输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
After 0 epoch,w is 2.600000,loss is 36.000000
After 1 epoch,w is 1.160000,loss is 12.959999
After 2 epoch,w is 0.296000,loss is 4.665599
After 3 epoch,w is -0.222400,loss is 1.679616
After 4 epoch,w is -0.533440,loss is 0.604662
After 5 epoch,w is -0.720064,loss is 0.217678
After 6 epoch,w is -0.832038,loss is 0.078364
After 7 epoch,w is -0.899223,loss is 0.028211
After 8 epoch,w is -0.939534,loss is 0.010156
After 9 epoch,w is -0.963720,loss is 0.003656
After 10 epoch,w is -0.978232,loss is 0.001316
After 11 epoch,w is -0.986939,loss is 0.000474
After 12 epoch,w is -0.992164,loss is 0.000171
After 13 epoch,w is -0.995298,loss is 0.000061
After 14 epoch,w is -0.997179,loss is 0.000022
After 15 epoch,w is -0.998307,loss is 0.000008
After 16 epoch,w is -0.998984,loss is 0.000003
After 17 epoch,w is -0.999391,loss is 0.000001
After 18 epoch,w is -0.999634,loss is 0.000000
After 19 epoch,w is -0.999781,loss is 0.000000
After 20 epoch,w is -0.999868,loss is 0.000000
After 21 epoch,w is -0.999921,loss is 0.000000
After 22 epoch,w is -0.999953,loss is 0.000000
After 23 epoch,w is -0.999972,loss is 0.000000
After 24 epoch,w is -0.999983,loss is 0.000000
After 25 epoch,w is -0.999990,loss is 0.000000
After 26 epoch,w is -0.999994,loss is 0.000000
After 27 epoch,w is -0.999996,loss is 0.000000
After 28 epoch,w is -0.999998,loss is 0.000000
After 29 epoch,w is -0.999999,loss is 0.000000
After 30 epoch,w is -0.999999,loss is 0.000000
After 31 epoch,w is -1.000000,loss is 0.000000
After 32 epoch,w is -1.000000,loss is 0.000000
After 33 epoch,w is -1.000000,loss is 0.000000
After 34 epoch,w is -1.000000,loss is 0.000000
After 35 epoch,w is -1.000000,loss is 0.000000
After 36 epoch,w is -1.000000,loss is 0.000000
After 37 epoch,w is -1.000000,loss is 0.000000
After 38 epoch,w is -1.000000,loss is 0.000000
After 39 epoch,w is -1.000000,loss is 0.000000

lr=0.001过慢

输出：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
After 0 epoch,w is 4.988000,loss is 36.000000
After 1 epoch,w is 4.976024,loss is 35.856144
After 2 epoch,w is 4.964072,loss is 35.712864
After 3 epoch,w is 4.952144,loss is 35.570156
After 4 epoch,w is 4.940240,loss is 35.428020
After 5 epoch,w is 4.928360,loss is 35.286449
After 6 epoch,w is 4.916503,loss is 35.145447
After 7 epoch,w is 4.904670,loss is 35.005009
After 8 epoch,w is 4.892860,loss is 34.865124
After 9 epoch,w is 4.881075,loss is 34.725803
After 10 epoch,w is 4.869313,loss is 34.587044
After 11 epoch,w is 4.857574,loss is 34.448833
After 12 epoch,w is 4.845859,loss is 34.311172
After 13 epoch,w is 4.834167,loss is 34.174068
After 14 epoch,w is 4.822499,loss is 34.037510
After 15 epoch,w is 4.810854,loss is 33.901497
After 16 epoch,w is 4.799233,loss is 33.766029
After 17 epoch,w is 4.787634,loss is 33.631104
After 18 epoch,w is 4.776059,loss is 33.496712
After 19 epoch,w is 4.764507,loss is 33.362858
After 20 epoch,w is 4.752978,loss is 33.229538
After 21 epoch,w is 4.741472,loss is 33.096756
After 22 epoch,w is 4.729989,loss is 32.964497
After 23 epoch,w is 4.718529,loss is 32.832775
After 24 epoch,w is 4.707092,loss is 32.701576
After 25 epoch,w is 4.695678,loss is 32.570904
After 26 epoch,w is 4.684287,loss is 32.440750
After 27 epoch,w is 4.672918,loss is 32.311119
After 28 epoch,w is 4.661572,loss is 32.182003
After 29 epoch,w is 4.650249,loss is 32.053402
After 30 epoch,w is 4.638949,loss is 31.925320
After 31 epoch,w is 4.627671,loss is 31.797745
After 32 epoch,w is 4.616416,loss is 31.670683
After 33 epoch,w is 4.605183,loss is 31.544128
After 34 epoch,w is 4.593973,loss is 31.418077
After 35 epoch,w is 4.582785,loss is 31.292530
After 36 epoch,w is 4.571619,loss is 31.167484
After 37 epoch,w is 4.560476,loss is 31.042938
After 38 epoch,w is 4.549355,loss is 30.918892
After 39 epoch,w is 4.538256,loss is 30.795341

lr=0.999不收敛

输出：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
After 0 epoch,w is -6.988000,loss is 36.000000
After 1 epoch,w is 4.976024,loss is 35.856144
After 2 epoch,w is -6.964072,loss is 35.712860
After 3 epoch,w is 4.952145,loss is 35.570156
After 4 epoch,w is -6.940241,loss is 35.428024
After 5 epoch,w is 4.928361,loss is 35.286461
After 6 epoch,w is -6.916504,loss is 35.145462
After 7 epoch,w is 4.904671,loss is 35.005020
After 8 epoch,w is -6.892861,loss is 34.865135
After 9 epoch,w is 4.881076,loss is 34.725815
After 10 epoch,w is -6.869314,loss is 34.587051
After 11 epoch,w is 4.857575,loss is 34.448849
After 12 epoch,w is -6.845860,loss is 34.311192
After 13 epoch,w is 4.834168,loss is 34.174084
After 14 epoch,w is -6.822500,loss is 34.037521
After 15 epoch,w is 4.810855,loss is 33.901508
After 16 epoch,w is -6.799233,loss is 33.766033
After 17 epoch,w is 4.787635,loss is 33.631107
After 18 epoch,w is -6.776060,loss is 33.496716
After 19 epoch,w is 4.764508,loss is 33.362869
After 20 epoch,w is -6.752979,loss is 33.229557
After 21 epoch,w is 4.741473,loss is 33.096771
After 22 epoch,w is -6.729990,loss is 32.964516
After 23 epoch,w is 4.718530,loss is 32.832787
After 24 epoch,w is -6.707093,loss is 32.701580
After 25 epoch,w is 4.695680,loss is 32.570911
After 26 epoch,w is -6.684288,loss is 32.440765
After 27 epoch,w is 4.672919,loss is 32.311131
After 28 epoch,w is -6.661573,loss is 32.182014
After 29 epoch,w is 4.650250,loss is 32.053413
After 30 epoch,w is -6.638950,loss is 31.925329
After 31 epoch,w is 4.627672,loss is 31.797762
After 32 epoch,w is -6.616417,loss is 31.670694
After 33 epoch,w is 4.605185,loss is 31.544140
After 34 epoch,w is -6.593974,loss is 31.418095
After 35 epoch,w is 4.582787,loss is 31.292547
After 36 epoch,w is -6.571621,loss is 31.167505
After 37 epoch,w is 4.560478,loss is 31.042959
After 38 epoch,w is -6.549357,loss is 30.918919
After 39 epoch,w is 4.538259,loss is 30.795368

指数衰减学习率

可以先用较大的学习率，快速得到较优解，然后逐步减小学习率，使模型在训练后期稳定。

初始学习率、学习率衰减率、多少轮衰减一次：超参数

当前轮数：变量、计数器，可以用当前跌倒了多少次数据集，也就是epoch数值表示；也可以用当前一共迭代了多少次batch也就是golobal_step表示

多少轮衰减一次：迭代多少次数据集，或者迭代多少次batch更新一次学习率；决定了学习率更新的频率

指数衰减学习率的计算一般写在for循环中

在上个代码中添加指数衰减学习率后

使得学习率根据迭代的轮数指数衰减了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import tensorflow as tf

w = tf.Variable(tf.constant(5, dtype=tf.float32))

epoch = 40

LR_BASE = 0.2  # 最初学习率
LR_DECAY = 0.99  # 学习率衰减率
LR_STEP = 1  # 喂入多少轮BATCH_SIZE后，更新一次学习率

for epoch in range(epoch):  # for epoch 定义顶层循环，表示对数据集循环epoch次，此例数据集数据仅有1个w,初始化时候constant赋值为5，循环100次迭代。
    lr = LR_BASE * LR_DECAY ** (epoch / LR_STEP)	#指数衰减学习率
    with tf.GradientTape() as tape:  # with结构到grads框起了梯度的计算过程。
        loss = tf.square(w + 1)
    grads = tape.gradient(loss, w)  # .gradient函数告知谁对谁求导

    w.assign_sub(lr * grads)  # .assign_sub 对变量做自减 即：w -= lr*grads 即 w = w - lr*grads
    print("After %s epoch,w is %f,loss is %f,lr is %f" % (epoch, w.numpy(), loss, lr))

运行结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
After 0 epoch,w is 2.600000,loss is 36.000000,lr is 0.200000
After 1 epoch,w is 1.174400,loss is 12.959999,lr is 0.198000
After 2 epoch,w is 0.321948,loss is 4.728015,lr is 0.196020
After 3 epoch,w is -0.191126,loss is 1.747547,lr is 0.194060
After 4 epoch,w is -0.501926,loss is 0.654277,lr is 0.192119
After 5 epoch,w is -0.691392,loss is 0.248077,lr is 0.190198
After 6 epoch,w is -0.807611,loss is 0.095239,lr is 0.188296
After 7 epoch,w is -0.879339,loss is 0.037014,lr is 0.186413
After 8 epoch,w is -0.923874,loss is 0.014559,lr is 0.184549
After 9 epoch,w is -0.951691,loss is 0.005795,lr is 0.182703
After 10 epoch,w is -0.969167,loss is 0.002334,lr is 0.180876
After 11 epoch,w is -0.980209,loss is 0.000951,lr is 0.179068
After 12 epoch,w is -0.987226,loss is 0.000392,lr is 0.177277
After 13 epoch,w is -0.991710,loss is 0.000163,lr is 0.175504
After 14 epoch,w is -0.994591,loss is 0.000069,lr is 0.173749
After 15 epoch,w is -0.996452,loss is 0.000029,lr is 0.172012
After 16 epoch,w is -0.997660,loss is 0.000013,lr is 0.170292
After 17 epoch,w is -0.998449,loss is 0.000005,lr is 0.168589
After 18 epoch,w is -0.998967,loss is 0.000002,lr is 0.166903
After 19 epoch,w is -0.999308,loss is 0.000001,lr is 0.165234
After 20 epoch,w is -0.999535,loss is 0.000000,lr is 0.163581
After 21 epoch,w is -0.999685,loss is 0.000000,lr is 0.161946
After 22 epoch,w is -0.999786,loss is 0.000000,lr is 0.160326
After 23 epoch,w is -0.999854,loss is 0.000000,lr is 0.158723
After 24 epoch,w is -0.999900,loss is 0.000000,lr is 0.157136
After 25 epoch,w is -0.999931,loss is 0.000000,lr is 0.155564
After 26 epoch,w is -0.999952,loss is 0.000000,lr is 0.154009
After 27 epoch,w is -0.999967,loss is 0.000000,lr is 0.152469
After 28 epoch,w is -0.999977,loss is 0.000000,lr is 0.150944
After 29 epoch,w is -0.999984,loss is 0.000000,lr is 0.149434
After 30 epoch,w is -0.999989,loss is 0.000000,lr is 0.147940
After 31 epoch,w is -0.999992,loss is 0.000000,lr is 0.146461
After 32 epoch,w is -0.999994,loss is 0.000000,lr is 0.144996
After 33 epoch,w is -0.999996,loss is 0.000000,lr is 0.143546
After 34 epoch,w is -0.999997,loss is 0.000000,lr is 0.142111
After 35 epoch,w is -0.999998,loss is 0.000000,lr is 0.140690
After 36 epoch,w is -0.999999,loss is 0.000000,lr is 0.139283
After 37 epoch,w is -0.999999,loss is 0.000000,lr is 0.137890
After 38 epoch,w is -0.999999,loss is 0.000000,lr is 0.136511
After 39 epoch,w is -0.999999,loss is 0.000000,lr is 0.135146

激活函数

鸢尾花的神经网络模型如下图所示，其激活函数是线性函数，即使增加网络层数，依旧为线性，模型的表达能力不够。

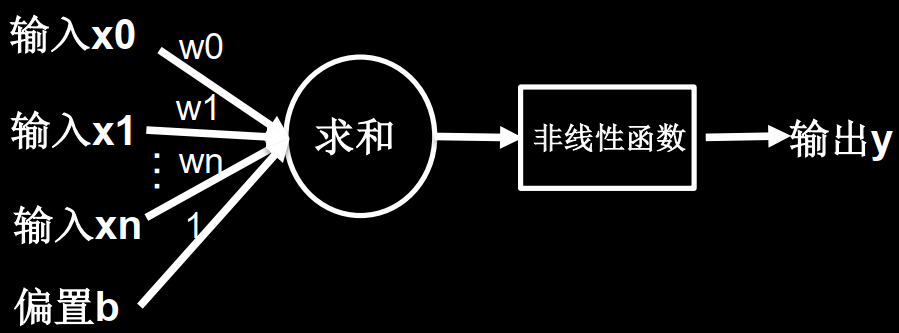
相较于线性网络结构，多了一个非线性函数，叫做激活函数，提升了模型的表达力。

使得网络不再是简单的线性组合，可以随着层数的增加提升表达能力。

优秀的激活函数

• 非线性： 激活函数非线性时，多层神经网络可逼近所有函数

• 可微性： 优化器大多用梯度下降更新参数

• 单调性： 当激活函数是单调的，能保证单层网络的损失函数是凸函数

• 近似恒等性： f(x)≈x当参数初始化为随机小值时，神经网络更稳定

激活函数输出值的范围

• 激活函数输出为有限值时，权重对特征的影响会更显著，基于梯度的优化方法更稳定

• 激活函数输出为无限值时，参数的初始值对模型的影响非常大，建议调小学习率

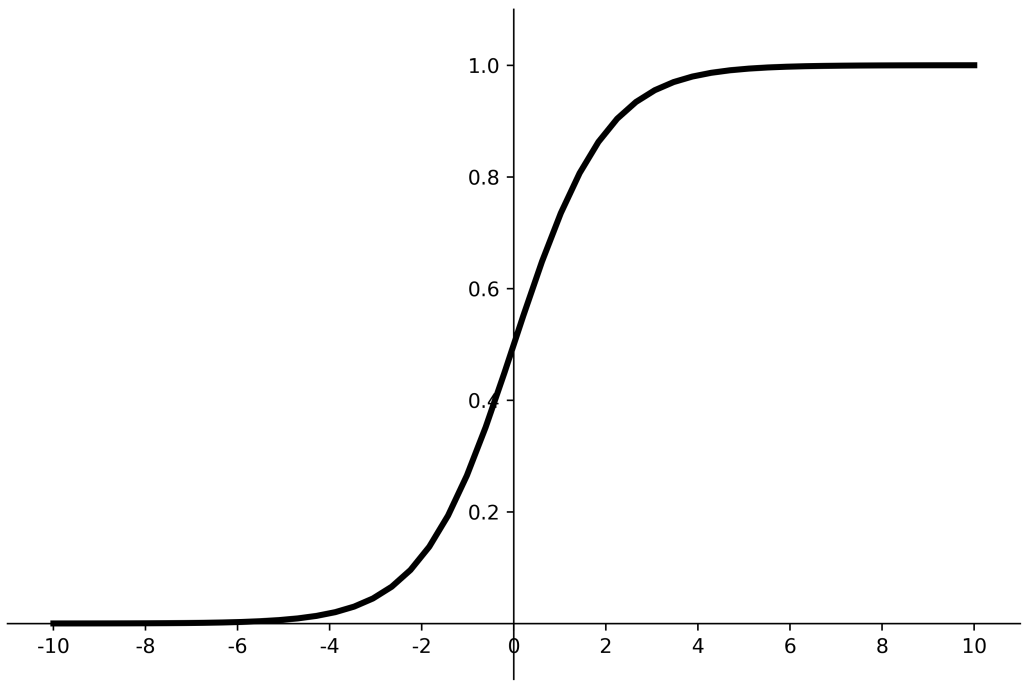
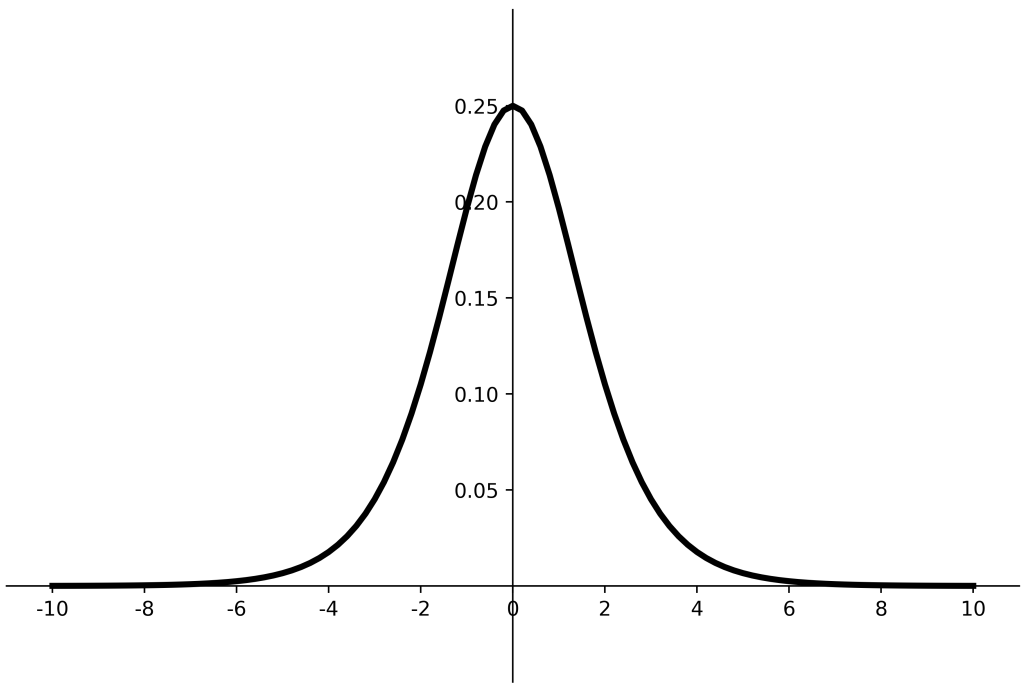
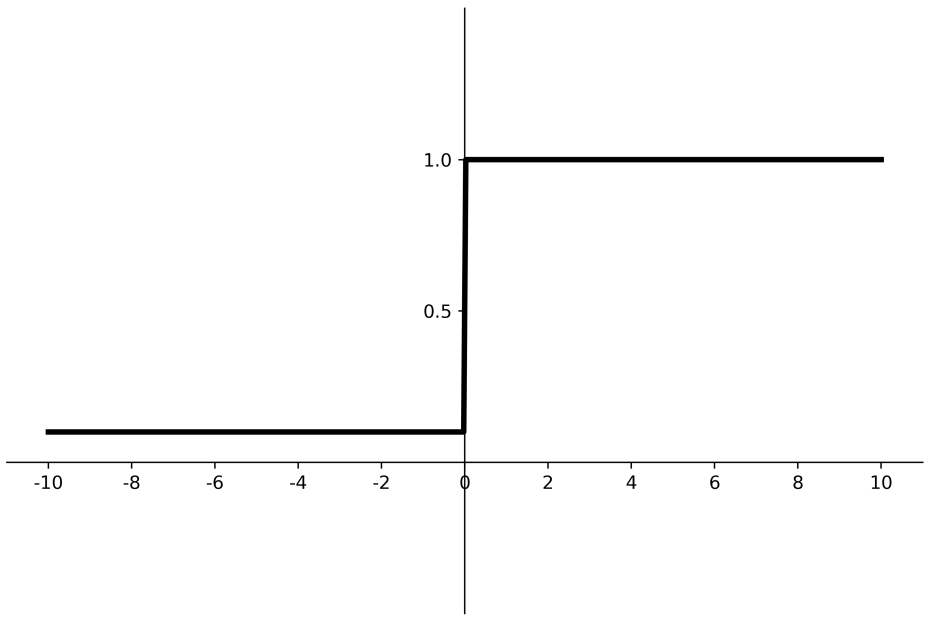
常用激活函数

Sigmoid函数

1
tf.nn.sigmoid(x)

Sigmoid函数把输入值变换到0~1之间输出

输入非常大的负数，为0；输入非常大的整数，为1。相当于归一化操作。

深层神经网络更新参数时，需要从输出层到输入层逐层进行链式求导。但Sigmoid函数的倒数输出是0~0.25之间的小数。会出现多个0到0.25之间的连续相乘，结果将趋近于0，产生梯度消失，使得参数无法继续更新。我们希望输入每层神经网络的特征是以0为均值的小数值。但是如果Sigmoid激活函数后的数据都是正数，会使得收敛变慢。另外，Sigmoid函数存在幂运算计算复杂度过大，训练时间长。

特点：

（1）易造成梯度消失

（2）输出非0均值，收敛慢

（3）幂运算复杂，训练时间长

Sigmoid函数API

1
2
3
tf.math.sigmoid(
	x, name = None
)
  • 功能：计算x每一个元素的Sigmoid值
  • 等价API：tf.nn.sigmoid, tf.sigmoid
  • 参数：
    x : 张量x
  • 返回：与x shape相同的张量
  • 案例：
1
2
3
4
5
6
7
x = tf.constant([1., 2., 3.], )
print(tf.math.sigmoid(x))
>>> tf.Tensor([0.7310586 0.880797 0.95257413], shape=(3,), dtype=float32)

>>> # 等价实现
print(1/(1+tf.math.exp(-x)))
>>> tf.Tensor([0.7310586 0.880797 0.95257413], shape=(3,), dtype=float32)

Tanh函数

1
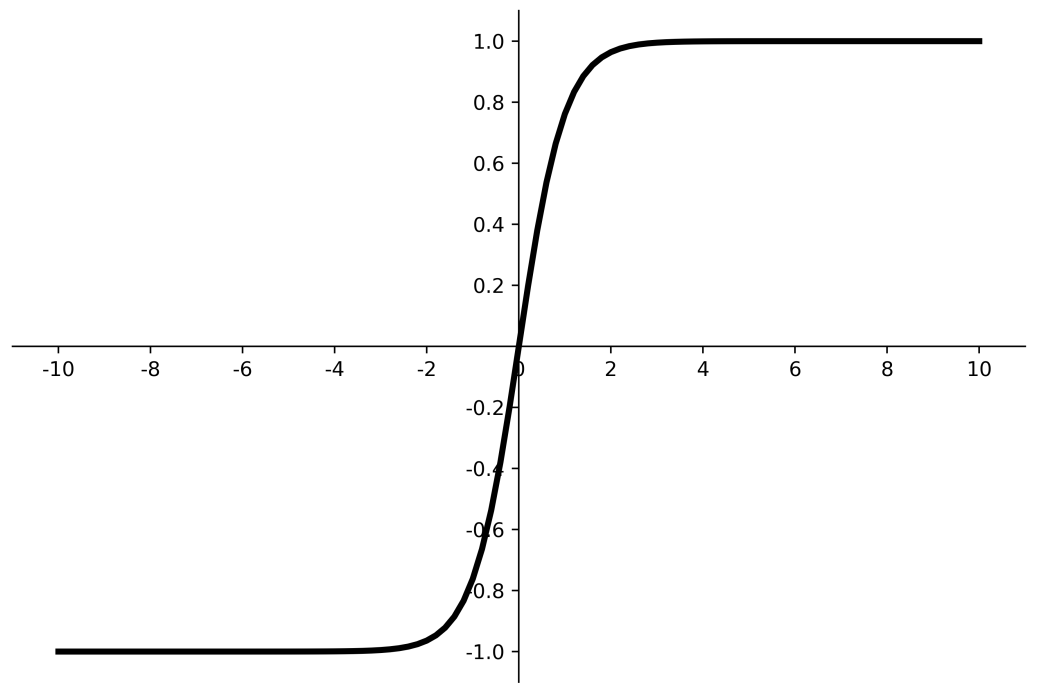
tf.math.tanh(x)

特点：

（1）输出是0均值

（2）易造成梯度消失

（3）幂运算复杂，训练时间长

Tanh函数API

1
2
3
tf.math.tanh(
	x, name = None
)
  • 功能：计算x每一个元素的Tanh值
  • 等价API：tf.nn.tanh, tf.tanh
  • 参数：
    x : 张量x
  • 返回：与x shape相同的张量
  • 案例：
1
2
3
4
5
6
7
8
9
x = tf.constant([-float("inf"), -5, -0.5, 1, 1.2, 2, 3, float("inf")])
print(tf.math.tanh(x))
>>> tf.Tensor([-1. -0.99990916 -0.46211717 0.7615942 0.8336547 0.9640276
0.9950547 1.], shape=(8,), dtype=float32)

# 等价实现
print((tf.math.exp(x)-tf.math.exp(-x))/(tf.math.exp(x)+tf.math.exp(-x)))
>>> tf.Tensor([nan -0.9999091 -0.46211714 0.7615942 0.83365464 0.9640275
0.9950547 nan], shape=(8,), dtype=float32)

Relu函数

1
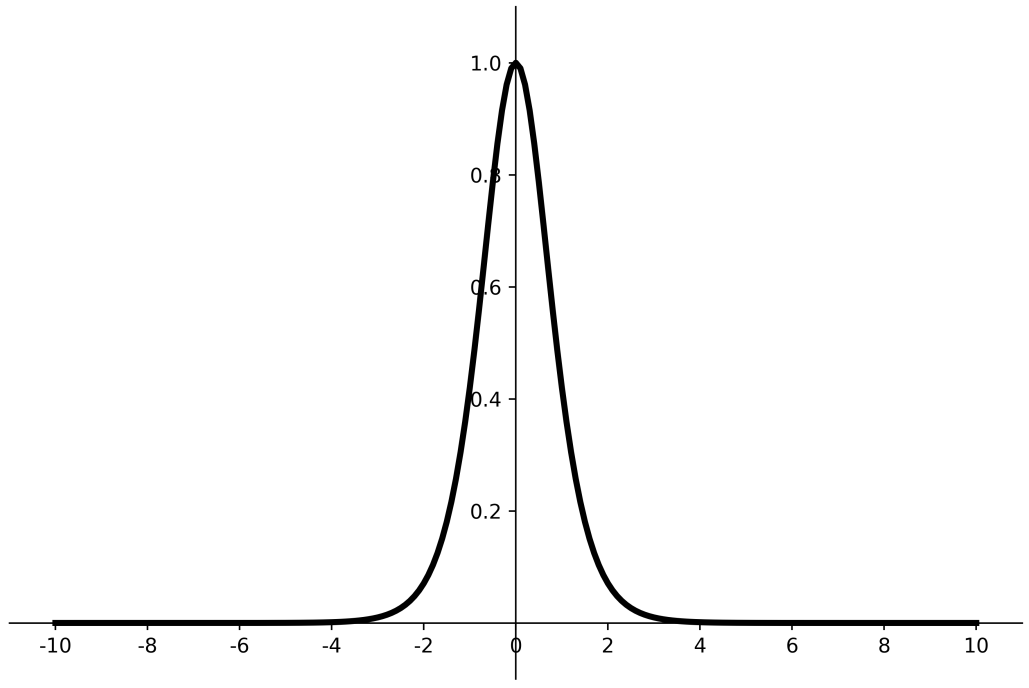
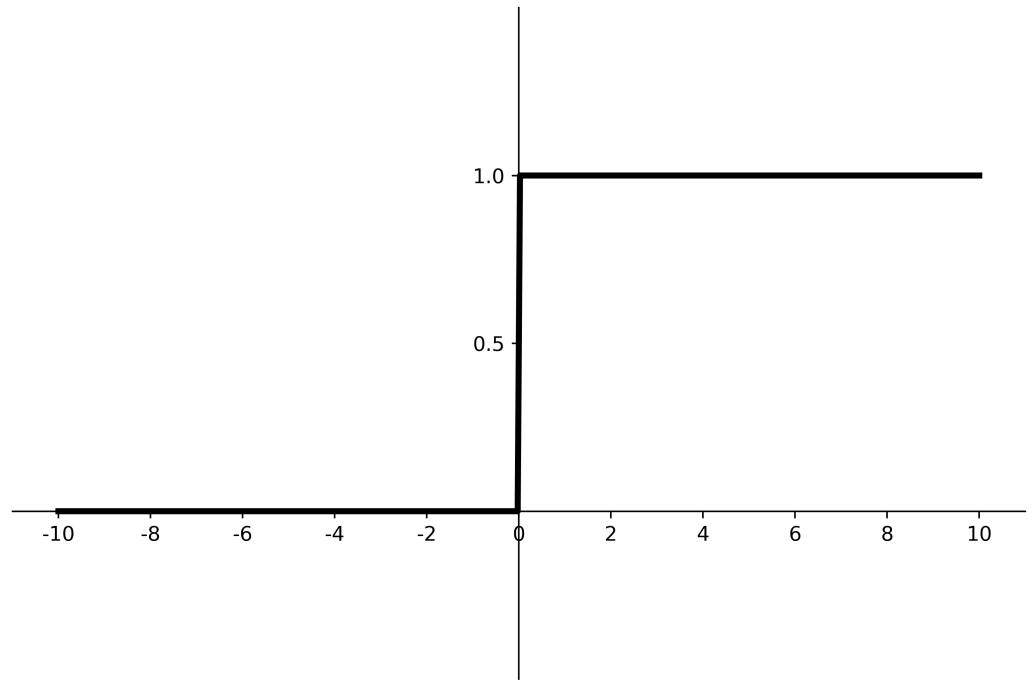
tf.nn.relu(x)

优点：

（1） 解决了梯度消失问题 (在正区间)

（2） 只需判断输入是否大于0，计算速度快

（3） 收敛速度远快于sigmoid和tanh

缺点：

（1） 输出非0均值，收敛慢

（2） Dead RelU问题：某些神经元可能永远不会被激活，导致相应的参数永远不能被更新。送入激活函数的输入特征是负数时，激活函数输出是0，反向传播得到的梯度是0，参数无法更新，神经元死亡。神经元死亡的原因是，经过relu函数的负数特征过多，可以改进随机初始化，避免过多的负数特征送入relu函数。可以通过设置更小的学习率，减少参数分布的巨大变化，避免训练中产生过多负数特征进入relu函数。

Relu函数API

1
2
3
tf.nn.relu(
	features, name = None
)
  • 功能：计算修正线性值(rectified linear)：max(features, 0).
  • 参数：
    features：张量
  • 返回：与features shape相同的张量
  • 例子：
1
2
print(tf.nn.relu([-2., 0., -0., 3.]))
>>> tf.Tensor([0. 0. -0. 3.], shape=(4,), dtype=float32)

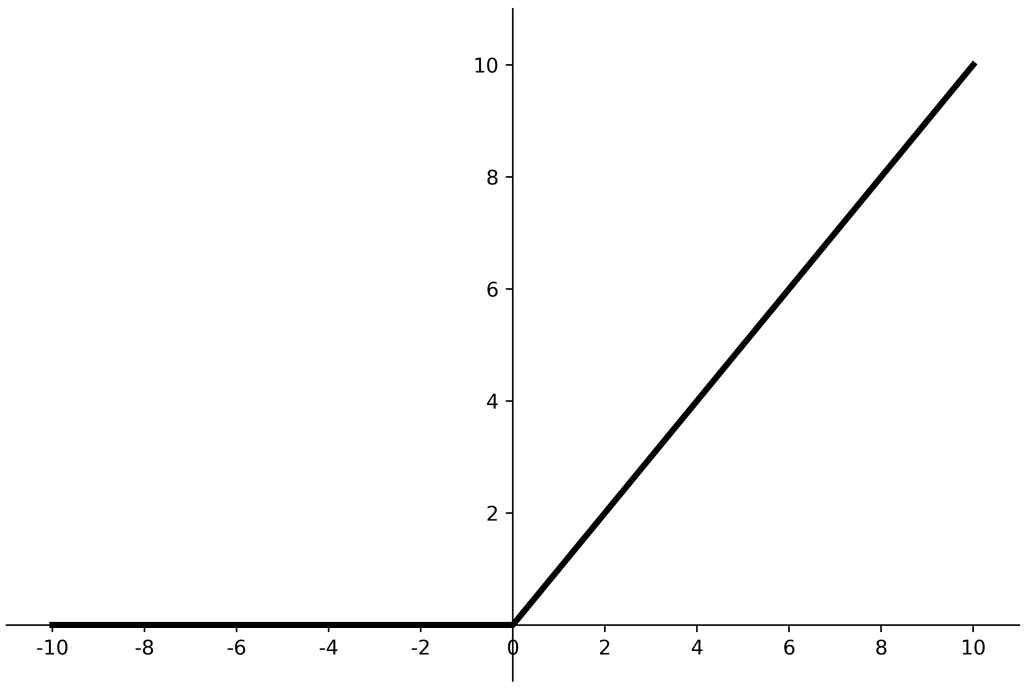
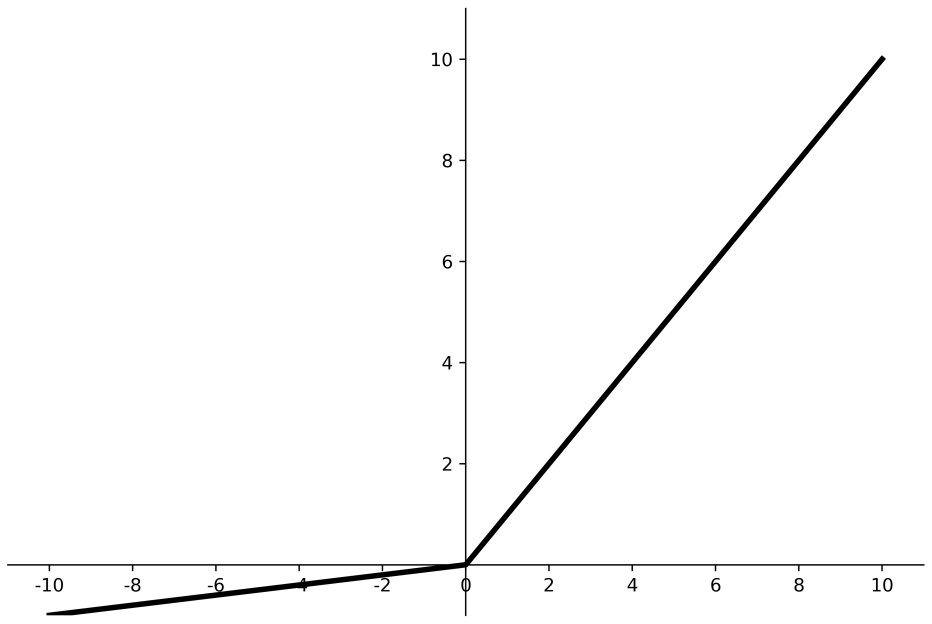
Leaky Relu函数

1
tf.nn.leaky_relu(x)

Leaky Relu函数是为了解决relu负区间为0，引起神经元死亡问题而设计的，Leaky Relu负区间引入了一个固定的斜率α，使得Leaky Relu负区间不再恒等于0。

理论上来讲， Leaky Relu有Relu的所有优点，外加不会有Dead Relu问题，但是在实际操作当中，并没有完全证明Leaky Relu总是好于Relu，选择Relu作为激活函数的网络会更多。

对于初学者的建议：

  • 首选relu激活函数；
  • 学习率设置较小值；
  • 输入特征标准化，即让输入特征满足以0为均值，1为标准差的正态分布；
  • 初始参数中心化，即让随机生成的参数满足以0为均值， $ \sqrt{\frac{2}{当前层输入特征个数}} $ 为标准差的正态分布。

Leaky Relu函数API

1
2
3
tf.nn.leaky_relu(
	features, alpha=0.2, name=None
)
  • 功能：计算 Leaky Relu值
  • 参数：
    features：张量
    alpha：x<0时的斜率值
  • 返回：与features shape相同的张量
  • 例子：
1
2
print(tf.nn.leaky_relu([-2., 0., -0., 3.]))
>>> tf.Tensor([-0.4 0. -0. 3.], shape=(4,), dtype=float32)

损失函数

损失函数(loss)：向前传播计算出的预测值(y)与已知答案( y_ )的差距

神经网络的优化目标就是找到某套参数，使得计算出来的结果y和已知标准答案 y_ 无限接近，也就是他们的差距loss值最小。

主流loss有三种计算方法：均方误差、自定义和交叉熵。

均方误差MSE

Tensorflow是这样实现均方误差损失函数计算的。

1
loss_mse = tf.reduce_mean(tf.square(y, y_))

MSE-API

1
2
3
tf.keras.losses.MSE(
	y_true, y_pred
)
  • 功能：计算y_true和y_pred的均方误差
  • 例子：
    1
    2
    3
    4
    5
    6
    7
    8
    y_true = tf.constant([0.5, 0.8])
    y_pred = tf.constant([1.0, 1.0])
    print(tf.keras.losses.MSE(y_true, y_pred))
    >>> tf.Tensor(0.145, shape=(), dtype=float32)

    # 等价实现
    print(tf.reduce_mean(tf.square(y_true - y_pred)))
    >>> tf.Tensor(0.145, shape=(), dtype=float32)

MSE案例

预测酸奶日销量y， x1、 x2是影响日销量的因素。
建模前，应预先采集的数据有：每日x1、 x2和销量y（即已知答案，最佳情况：产量=销量）
拟造数据集 X,Y： y_ = x1 + x2 噪声： -0.05 ~ +0.05 拟合可以预测销量的函数

缺少数据集自己造，一层神经网络，预测酸奶的日销量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import tensorflow as tf
import numpy as np

SEED = 23455

rdm = np.random.RandomState(seed=SEED)  # 生成[0,1)之间的随机数
x = rdm.rand(32, 2)
y_ = [[x1 + x2 + (rdm.rand() / 10.0 - 0.05)] for (x1, x2) in x]  # 生成噪声[0,1)/10=[0,0.1); [0,0.1)-0.05=[-0.05,0.05)
x = tf.cast(x, dtype=tf.float32)

w1 = tf.Variable(tf.random.normal([2, 1], stddev=1, seed=1))

epoch = 15000
lr = 0.002

for epoch in range(epoch):
    with tf.GradientTape() as tape:
        y = tf.matmul(x, w1)
        loss_mse = tf.reduce_mean(tf.square(y_ - y))

    grads = tape.gradient(loss_mse, w1)
    w1.assign_sub(lr * grads)

    if epoch % 500 == 0:
        print("After %d training steps,w1 is " % (epoch))
        print(w1.numpy(), "\n")
print("Final w1 is: ", w1.numpy())

运行结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
After 0 training steps,w1 is 
[[-0.8096241]
 [ 1.4855157]] 

...

After 3000 training steps,w1 is 
[[0.61725086]
 [1.332841  ]] 

...

After 6000 training steps,w1 is 
[[0.88665503]
 [1.098054  ]] 

...

After 10000 training steps,w1 is 
[[0.9801975]
 [1.0159837]] 

...

After 12000 training steps,w1 is 
[[0.9933934]
 [1.0044063]] 

...

Final w1 is:  [[1.0009792]
 [0.9977485]]

两个参数正向着1趋近，最后得到神经网络的参数是接近1的。

最终拟合结果：

结果和制造数据集的公式一致。

自定义损失函数

使用均方误差使用损失函数，默认认为销量预测的多了或者少了，损失是一样的。

而真实情况是，商品销量预测多了，损失的是成本；预测少了，损失的是利润。

利润和成本往往不相等，则MSE产生的loss不能使得利益最大化。

使用自定义损失函数，用自定义损失函数计算每一个预测结果y与标准答案 y_ 产生的损失累积和。

y_ ：标准答案数据集
y：预测答案计算出的

可以把损失定义为一个分段函数，如果预测的结果y小于标准答案 y_ ，则预测的y少了，损失的是利润。

自己写出一个损失函数

1
loss_zdy = tf.reduce_sum(tf.where(tf.greater(y, y_), COST * (y-y_), PROFIT * (y_-y)))

如：预测酸奶销量，酸奶成本（COST） 1元，酸奶利润（PROFIT） 99元。预测少了损失利润99元，大于预测多了损失成本1元。预测少了损失大，希望生成的预测函数往多了预测。

自定义损失函数案例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import tensorflow as tf
import numpy as np

SEED = 23455
COST = 1
PROFIT = 99

rdm = np.random.RandomState(SEED)
x = rdm.rand(32, 2)
y_ = [[x1 + x2 + (rdm.rand() / 10.0 - 0.05)] for (x1, x2) in x]  # 生成噪声[0,1)/10=[0,0.1); [0,0.1)-0.05=[-0.05,0.05)
x = tf.cast(x, dtype=tf.float32)

w1 = tf.Variable(tf.random.normal([2, 1], stddev=1, seed=1))

epoch = 10000
lr = 0.002

for epoch in range(epoch):
    with tf.GradientTape() as tape:
        y = tf.matmul(x, w1)
        loss = tf.reduce_sum(tf.where(tf.greater(y, y_), (y - y_) * COST, (y_ - y) * PROFIT))

    grads = tape.gradient(loss, w1)
    w1.assign_sub(lr * grads)

    if epoch % 500 == 0:
        print("After %d training steps,w1 is " % (epoch))
        print(w1.numpy(), "\n")
print("Final w1 is: ", w1.numpy())

# 自定义损失函数
# 酸奶成本1元， 酸奶利润99元
# 成本很低，利润很高，人们希望多预测些，生成模型系数大于1，往多了预测

运行结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
After 0 training steps,w1 is 
[[2.0855923]
 [3.8476257]] 

After 500 training steps,w1 is 
[[1.1830753]
 [1.1627482]] 

After 1000 training steps,w1 is 
[[1.1526372]
 [1.0175619]] 

...

After 6000 training steps,w1 is 
[[1.1528853]
 [1.1765157]] 

... 

After 9500 training steps,w1 is 
[[1.1611756]
 [1.0651482]] 

Final w1 is:  [[1.1626335]
 [1.1191947]]

当cost=1，profit=99时，两个参数都大于1，都大于用均方误差做损失函数时的系数，模型在尽量往多了预测。

最终拟合结果：

当cost=99，profit=1时，结果两个参数均小于1，模型在尽量往少了预测。

最终拟合结果：

交叉熵

交叉熵损失函数CE (Cross Entropy)：表征两个概率分布之间的距离。

交叉熵越大，两个概率分布越远；交叉熵越小，两个概率分布越近。

y_ : 真实结果的概率分布
y：预测结果的概率分布

通过交叉熵的值可以判断哪一个预测结果和标准答案更接近。

交叉熵损失函数案例

二分类 已知答案 y_ = (1, 0) 预测 y1=(0.6, 0.4) 和 y2=(0.8, 0.2) 哪个更接近标准答案？

因为H1 > H2，所以y2预测更准

1
tf.losses.categorical_crossentropy(y_, y)
1
2
3
4
loss_ce1=tf.losses.categorical_crossentropy([1, 0], [0.6, 0.4])
loss_ce2=tf.losses.categorical_crossentropy([1, 0], [0.8, 0.2])
print("loss_ce1:", loss_ce1)
print("loss_ce2:", loss_ce2)

运行结果：

1
2
loss_ce1: tf.Tensor(0.5108256, shape=(), dtype=float32)
loss_ce2: tf.Tensor(0.22314353, shape=(), dtype=float32)

交叉熵-API

softmax-API

1
2
3
tf.nn.softmax(
	logits, axis=None, name=None
)
  • 功能：计算softmax激活值
  • 等价API：tf.math.softmax
  • 参数：
    logits：张量
    axis：计算softmax所在的维度，默认为-1，即最后一个维度
  • 返回：与logits shape相同的张量
  • 例子：
1
2
3
4
5
6
7
logits = tf.constant([4., 5., 1.])
print(tf.nn.softmax(logits))
>>> tf.Tensor([0.26538792 0.7213992 0.01321289], shape=(3,), dtype=float32)

# 等价实现
print(tf.exp(logits) / tf.reduce_sum(tf.exp(logits)))
>>> tf.Tensor([0.26538792 0.72139925 0.01321289], shape=(3,), dtype=float32)

tf.keras.losses.categorical_crossentropy

1
2
3
tf.keras.losses.categorical_crossentropy(
	y_true, y_pred, from_logits=False, label_smoothing=0
)
  • 功能：计算交叉熵
  • 等价API：tf.losses.categorical_crossentropy
  • 参数：
    y_true：真实值
    y_pred：预测值
    from_logits：y_pred是否为logits张量
    label_smoothing：[0, 1]之间的小数
  • 返回：交叉熵损失值
  • 例子：
1
2
3
4
5
6
7
8
9
10
11
12
13
y_true = [1, 0, 0]
y_pred1 = [0.5, 0.4, 0.1]
y_pred2 = [0.8, 0.1, 0.1]
print(tf.keras.losses.categorical_crossentropy(y_true, y_pred1))
print(tf.keras.losses.categorical_crossentropy(y_true, y_pred2))
>>> tf.Tensor(0.6931472, shape=(), dtype=float32)
tf.Tensor(0.22314353, shape=(), dtype=float32)

# 等价实现
print(-tf.reduce_sum(y_true * tf.math.log(y_pred1)))
print(-tf.reduce_sum(y_true * tf.math.log(y_pred2)))
>>> tf.Tensor(0.6931472, shape=(), dtype=float32)
tf.Tensor(0.22314353, shape=(), dtype=float32)

tf.nn.softmax_cross_entropy_with_logits

1
2
3
tf.nn.softmax_cross_entropy_with_logits(
	labels, logits, axis=-1, name=None
)

在机器学习中，对于多分类问题，把未经softmax归一化的向量值称为logits。logits经过softmax
层后，输出服从概率分布的向量。

  • 功能：logits经过softmax后，与labels进行交叉熵计算
  • 参数：
    labels：:在类别这一维度上，每个向量应服从有效的概率分布。例如，在labels的shape为[batch_size, num_classes]的情况下，labels[i]应服从概率分布。
    logits：每个类别的激活值，通常是线性层的输出. 激活值需要经过softmax归一化。
    axis: 类别所在维度，默认是-1，即最后一个维度。
  • 返回：softmax交叉熵损失值。
  • 例子：
1
2
3
4
5
6
7
8
labels = [[1.0, 0.0, 0.0], [0.0, 1.0, 0.0]]
logits = [[4.0, 2.0, 1.0], [0.0, 5.0, 1.0]]
print(tf.nn.softmax_cross_entropy_with_logits(labels=labels, logits=logits))
>>> tf.Tensor([0.16984604 0.02474492], shape=(2,), dtype=float32)

# 等价实现
print(-tf.reduce_sum(labels * tf.math.log(tf.nn.softmax(logits)), axis=1))
>>> tf.Tensor([0.16984606 0.02474495], shape=(2,), dtype=float32)

tf.nn.sparse_softmax_cross_entropy_with_logits

1
2
3
tf.nn.sparse_softmax_cross_entropy_with_logits(
	labels, logits, name=None
)
  • 功能：labels经过one-hot编码，logits经过softmax，两者进行交叉熵计算。通常labels的shape为[batch_size]，logits的shape为[batch_size, num_classes]。sparse可理解为对labels进行稀疏化处理(即进行one-hot编码)
  • 参数：
    labels：标签的索引值
    logits：每个类别的激活值，通常是线性层的输出。激活值需要经过softmax归一化。
  • 返回：softmax交叉熵损失值
  • 例子：（下例中先对labels进行one-hot编码为[[1,0,0], [0,1,0]]，logits经过softmax变为[[0.844，
    0.114，0.042], [0.007, 0.976, 0.018]]，两者再进行交叉熵运算）
1
2
3
4
5
6
7
8
labels = [0, 1]
logits = [[4.0, 2.0, 1.0], [0.0, 5.0, 1.0]]
print(tf.nn.sparse_softmax_cross_entropy_with_logits(labels1, logits))
>>> tf.Tensor([0.16984604 0.02474492], shape=(2,), dtype=float32)

# 等价实现
print(-tf.reduce_sum(tf.one_hot(labels, tf.shape(logits)[1]) * tf.math.log(tf.nn.softmax(logits)), axis=1))
>>> tf.Tensor([0.16984606 0.02474495], shape=(2,), dtype=float32)

softmax与交叉熵结合

输出先过softmax函数，再计算 y 与 y_ 的交叉熵损失函数。

同时计算概率分布和交叉熵的函数

1
tf.nn.softmax_cross_entropy_with_logits(y_， y)
1
2
3
4
5
6
7
8
9
10
11
12
# softmax与交叉熵损失函数的结合
import tensorflow as tf
import numpy as np

y_ = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1], [1, 0, 0], [0, 1, 0]])
y = np.array([[12, 3, 2], [3, 10, 1], [1, 2, 5], [4, 6.5, 1.2], [3, 6, 1]])
y_pro = tf.nn.softmax(y)
loss_ce1 = tf.losses.categorical_crossentropy(y_,y_pro)
loss_ce2 = tf.nn.softmax_cross_entropy_with_logits(y_, y)

print('分步计算的结果:\n', loss_ce1)
print('结合计算的结果:\n', loss_ce2)

运行结果：

1
2
3
4
5
6
7
8
分步计算的结果:
 tf.Tensor(
[1.68795487e-04 1.03475622e-03 6.58839038e-02 2.58349207e+00
 5.49852354e-02], shape=(5,), dtype=float64)
结合计算的结果:
 tf.Tensor(
[1.68795487e-04 1.03475622e-03 6.58839038e-02 2.58349207e+00
 5.49852354e-02], shape=(5,), dtype=float64)

缓解过拟合

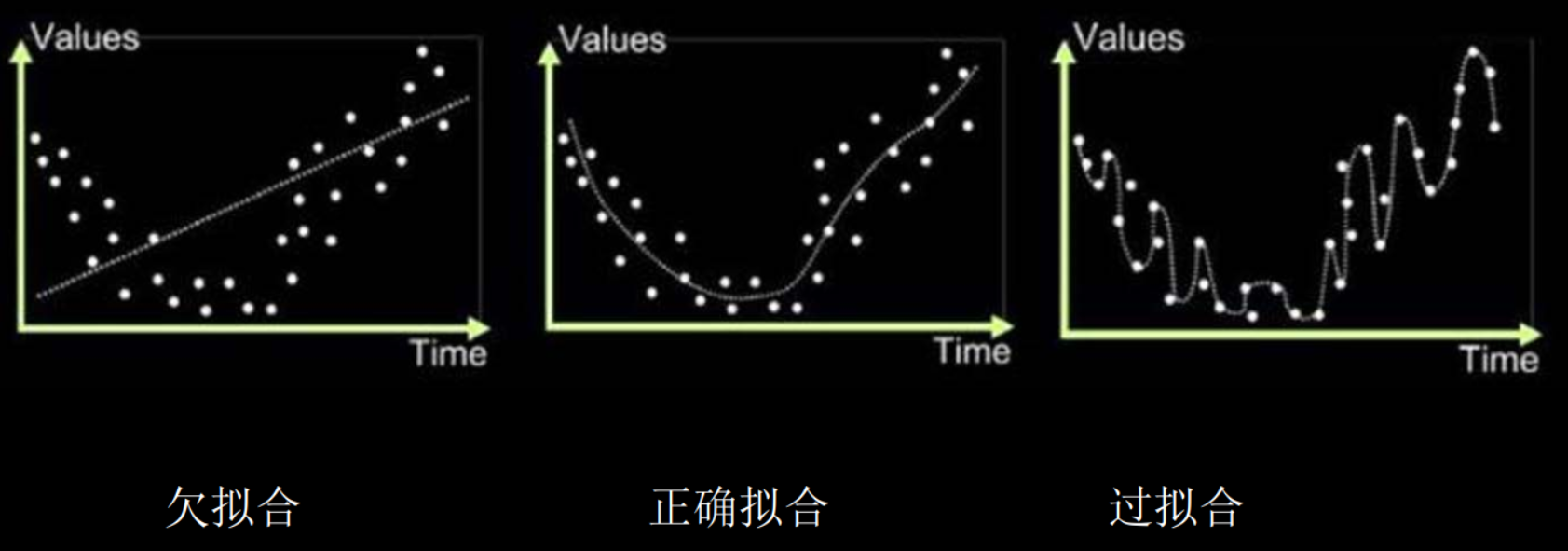
  • 欠拟合：对现有数据集学习的不够彻底
  • 过拟合：模型对当前数据拟合得太好了，但对未出现的新数据难以做出正确的判断，模型缺少泛化能力

欠拟合的解决方法

  • 增加输入特征项
  • 增加网络参数
  • 减少正则化参数

过拟合的解决方法

  • 数据清洗
  • 增大训练集
  • 采用正则化
  • 增大正则化参数

正则化缓解过拟合

正则化在损失函数中引入模型复杂度指标，利用给W加权值，弱化了训练数据的噪声（一般不正则化b）

使用正则化后，损失函数loss变成两部分的和。

第一部分是以前求得的loss值，描述了预测结果和正确结果之间的差距，比如交叉熵，均方误差等。

第二部分是参数的权重，REGULARIZER给出参数w在总loss中的比例，正则化的权重。

loss(w)的计算可以使用两种方法

一种是对所有参数的w的绝对值求和，L1正则化。

L1正则化大概率会使很多参数变为零，因此该方法可通过稀疏参数，即减少参数的数量，降低复杂度。

二种是对所有参数的w平方求和，L2正则化。

L2正则化会使参数很接近零但不为零，因此该方法可通过减小参数值的大小降低复杂度。可以有效缓解数据集中由于噪声引起的过拟合。

L2正则化计算W过程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
with tf.GradientTape() as tape: # 记录梯度信息
	h1 = tf.matmul(x_train, w1) + bl #记录神经网络乘加运算
	h1 = tf.nn.relu(h1)
	y = tf.matmul(h1, w2) + b2
	
	#采用均方误差损失函数mse=mean(sum(y-out)^2)
	loss_mse = tf.reduce_mean(tf.square(y_train - y))
    
    #添加12正则化
    loss_regularization = []
    loss_reqularization.append(tf.nn.12_loss(w1))
    loss_regularization.append(tf.nn.12_loss(w2))
    loss_regularization = tf.reduce_sum(loss_regularization) 
    loss = loss_mse + 0.03 * loss_reqularization #REGULARIZER = 0.03

#计算loss对各个参数的梯度
variables = [w1, b1, w2, b2]
grads = tape.gradient(loss, variables)

测试数据

输入数据：

x1和x2是输入特征，y_c是标签

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
x1,x2,y_c
-0.416757847,-0.056266827,1
-2.136196096,1.640270808,0
-1.793435585,-0.841747366,0
0.502881417,-1.245288087,1
-1.057952219,-0.909007615,1
0.551454045,2.292208013,0
0.041539393,-1.117925445,1
0.539058321,-0.5961597,1
-0.019130497,1.17500122,1
-0.747870949,0.009025251,1
-0.878107893,-0.15643417,1
0.256570452,-0.988779049,1
-0.338821966,-0.236184031,1
-0.637655012,-1.187612286,1
-1.421217227,-0.153495196,0
-0.26905696,2.231366789,0
-2.434767577,0.112726505,0
0.370444537,1.359633863,1
0.501857207,-0.844213704,1
9.76E-06,0.542352572,1
-0.313508197,0.771011738,1
-1.868090655,1.731184666,0
1.467678011,-0.335677339,0
0.61134078,0.047970592,1
-0.829135289,0.087710218,1
1.000365887,-0.381092518,1
-0.375669423,-0.074470763,1
0.43349633,1.27837923,1

x1和x2作为横纵坐标可视化，标签为1是红色，标签为0是蓝色

先用神经网络拟合出输入特征x1、x2与标签的函数关系，生成网格覆盖这些点。

讲这些网格的交点也就是横纵坐标作为输入送入训练好的神经网络，神经网络会输出一个值，我们要区分输出偏向1还是偏向0。

可以把神经网络输出的预测值为0.5的线标出颜色。也就是红蓝点的区分线。

p29_regularizationfree.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
# 导入所需模块
import tensorflow as tf
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd

# 读入数据/标签 生成x_train y_train
df = pd.read_csv('dot.csv')
x_data = np.array(df[['x1', 'x2']])
y_data = np.array(df['y_c'])

x_train = np.vstack(x_data).reshape(-1,2)
y_train = np.vstack(y_data).reshape(-1,1)

Y_c = [['red' if y else 'blue'] for y in y_train]

# 转换x的数据类型，否则后面矩阵相乘时会因数据类型问题报错
x_train = tf.cast(x_train, tf.float32)
y_train = tf.cast(y_train, tf.float32)

# from_tensor_slices函数切分传入的张量的第一个维度，生成相应的数据集，使输入特征和标签值一一对应
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)

# 生成神经网络的参数，输入层为2个神经元，隐藏层为11个神经元，1层隐藏层，输出层为1个神经元
# 用tf.Variable()保证参数可训练
w1 = tf.Variable(tf.random.normal([2, 11]), dtype=tf.float32)
b1 = tf.Variable(tf.constant(0.01, shape=[11]))

w2 = tf.Variable(tf.random.normal([11, 1]), dtype=tf.float32)
b2 = tf.Variable(tf.constant(0.01, shape=[1]))

lr = 0.01  # 学习率
epoch = 400  # 循环轮数

# 训练部分
for epoch in range(epoch):
    for step, (x_train, y_train) in enumerate(train_db):
        with tf.GradientTape() as tape:  # 记录梯度信息

            h1 = tf.matmul(x_train, w1) + b1  # 记录神经网络乘加运算
            h1 = tf.nn.relu(h1)
            y = tf.matmul(h1, w2) + b2

            # 采用均方误差损失函数mse = mean(sum(y-out)^2)
            loss = tf.reduce_mean(tf.square(y_train - y))

        # 计算loss对各个参数的梯度
        variables = [w1, b1, w2, b2]
        grads = tape.gradient(loss, variables)

        # 实现梯度更新
        # w1 = w1 - lr * w1_grad tape.gradient是自动求导结果与[w1, b1, w2, b2] 索引为0，1，2，3 
        w1.assign_sub(lr * grads[0])
        b1.assign_sub(lr * grads[1])
        w2.assign_sub(lr * grads[2])
        b2.assign_sub(lr * grads[3])

    # 每20个epoch，打印loss信息
    if epoch % 20 == 0:
        print('epoch:', epoch, 'loss:', float(loss))

# 预测部分
print("*******predict*******")
# xx在-3到3之间以步长为0.01，yy在-3到3之间以步长0.01,生成间隔数值点
xx, yy = np.mgrid[-3:3:.1, -3:3:.1]
# 将xx , yy拉直，并合并配对为二维张量，生成二维坐标点
grid = np.c_[xx.ravel(), yy.ravel()]
grid = tf.cast(grid, tf.float32)
# 将网格坐标点喂入神经网络，进行预测，probs为输出
probs = []
for x_test in grid:
    # 使用训练好的参数进行预测
    h1 = tf.matmul([x_test], w1) + b1
    h1 = tf.nn.relu(h1)
    y = tf.matmul(h1, w2) + b2  # y为预测结果
    probs.append(y)

# 取第0列给x1，取第1列给x2
x1 = x_data[:, 0]
x2 = x_data[:, 1]
# probs的shape调整成xx的样子
probs = np.array(probs).reshape(xx.shape)
plt.scatter(x1, x2, color=np.squeeze(Y_c)) #squeeze去掉纬度是1的纬度,相当于去掉[['red'],[''blue]],内层括号变为['red','blue']
# 把坐标xx yy和对应的值probs放入contour<[‘kɑntʊr]>函数，给probs值为0.5的所有点上色  plt点show后 显示的是红蓝点的分界线
plt.contour(xx, yy, probs, levels=[.5])
plt.show()

# 读入红蓝点，画出分割线，不包含正则化
# 不清楚的数据，建议print出来查看 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
epoch: 0 loss: 0.8860995173454285
epoch: 20 loss: 0.07788623124361038
epoch: 40 loss: 0.05887502059340477
epoch: 60 loss: 0.043619509786367416
epoch: 80 loss: 0.03502746298909187
epoch: 100 loss: 0.03013235330581665
epoch: 120 loss: 0.027722788974642754
epoch: 140 loss: 0.026683270931243896
epoch: 160 loss: 0.026026234030723572
epoch: 180 loss: 0.025885531678795815
epoch: 200 loss: 0.025877559557557106
epoch: 220 loss: 0.02594858966767788
epoch: 240 loss: 0.026042431592941284
epoch: 260 loss: 0.026121510192751884
epoch: 280 loss: 0.026135003194212914
epoch: 300 loss: 0.026035090908408165
epoch: 320 loss: 0.02597750537097454
epoch: 340 loss: 0.025903111323714256
epoch: 360 loss: 0.025866234675049782
epoch: 380 loss: 0.02591524086892605

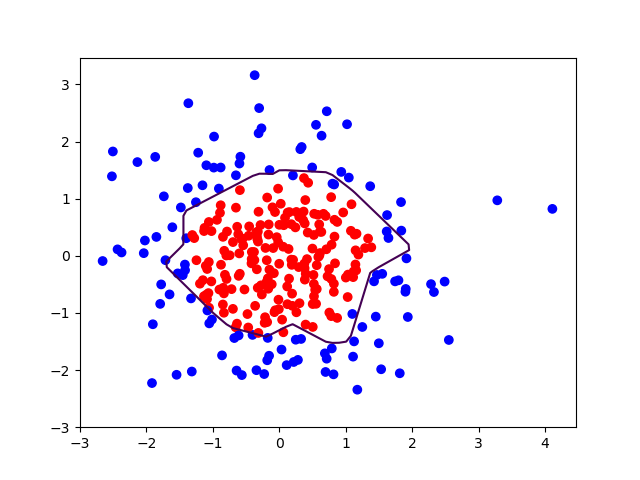
轮廓不够平滑，存在过拟合现象。

加入L2正则化：

p29_regularizationcontain.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
# 导入所需模块
import tensorflow as tf
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd

# 读入数据/标签 生成x_train y_train
df = pd.read_csv('dot.csv')
x_data = np.array(df[['x1', 'x2']])
y_data = np.array(df['y_c'])

x_train = x_data
y_train = y_data.reshape(-1, 1)

Y_c = [['red' if y else 'blue'] for y in y_train]

# 转换x的数据类型，否则后面矩阵相乘时会因数据类型问题报错
x_train = tf.cast(x_train, tf.float32)
y_train = tf.cast(y_train, tf.float32)

# from_tensor_slices函数切分传入的张量的第一个维度，生成相应的数据集，使输入特征和标签值一一对应
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)

# 生成神经网络的参数，输入层为4个神经元，隐藏层为32个神经元，2层隐藏层，输出层为3个神经元
# 用tf.Variable()保证参数可训练
w1 = tf.Variable(tf.random.normal([2, 11]), dtype=tf.float32)
b1 = tf.Variable(tf.constant(0.01, shape=[11]))

w2 = tf.Variable(tf.random.normal([11, 1]), dtype=tf.float32)
b2 = tf.Variable(tf.constant(0.01, shape=[1]))

lr = 0.01  # 学习率为
epoch = 400  # 循环轮数

# 训练部分
for epoch in range(epoch):
    for step, (x_train, y_train) in enumerate(train_db):
        with tf.GradientTape() as tape:  # 记录梯度信息

            h1 = tf.matmul(x_train, w1) + b1  # 记录神经网络乘加运算
            h1 = tf.nn.relu(h1)
            y = tf.matmul(h1, w2) + b2

            # 采用均方误差损失函数mse = mean(sum(y-out)^2)
            loss_mse = tf.reduce_mean(tf.square(y_train - y))
            # 添加l2正则化
            loss_regularization = []
            # tf.nn.l2_loss(w)=sum(w ** 2) / 2
            loss_regularization.append(tf.nn.l2_loss(w1))
            loss_regularization.append(tf.nn.l2_loss(w2))
            # 求和
            # 例：x=tf.constant(([1,1,1],[1,1,1]))
            # tf.reduce_sum(x)
            # >>>6
            # loss_regularization = tf.reduce_sum(tf.stack(loss_regularization))
            loss_regularization = tf.reduce_sum(loss_regularization)
            loss = loss_mse + 0.03 * loss_regularization #REGULARIZER = 0.03

        # 计算loss对各个参数的梯度
        variables = [w1, b1, w2, b2]
        grads = tape.gradient(loss, variables)

        # 实现梯度更新
        # w1 = w1 - lr * w1_grad
        w1.assign_sub(lr * grads[0])
        b1.assign_sub(lr * grads[1])
        w2.assign_sub(lr * grads[2])
        b2.assign_sub(lr * grads[3])

    # 每200个epoch，打印loss信息
    if epoch % 20 == 0:
        print('epoch:', epoch, 'loss:', float(loss))

# 预测部分
print("*******predict*******")
# xx在-3到3之间以步长为0.01，yy在-3到3之间以步长0.01,生成间隔数值点
xx, yy = np.mgrid[-3:3:.1, -3:3:.1]
# 将xx, yy拉直，并合并配对为二维张量，生成二维坐标点
grid = np.c_[xx.ravel(), yy.ravel()]
grid = tf.cast(grid, tf.float32)
# 将网格坐标点喂入神经网络，进行预测，probs为输出
probs = []
for x_predict in grid:
    # 使用训练好的参数进行预测
    h1 = tf.matmul([x_predict], w1) + b1
    h1 = tf.nn.relu(h1)
    y = tf.matmul(h1, w2) + b2  # y为预测结果
    probs.append(y)

# 取第0列给x1，取第1列给x2
x1 = x_data[:, 0]
x2 = x_data[:, 1]
# probs的shape调整成xx的样子
probs = np.array(probs).reshape(xx.shape)
plt.scatter(x1, x2, color=np.squeeze(Y_c))
# 把坐标xx yy和对应的值probs放入contour<[‘kɑntʊr]>函数，给probs值为0.5的所有点上色  plt点show后 显示的是红蓝点的分界线
plt.contour(xx, yy, probs, levels=[.5])
plt.show()

# 读入红蓝点，画出分割线，包含正则化
# 不清楚的数据，建议print出来查看 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
epoch: 0 loss: 1.187268853187561
epoch: 20 loss: 0.4623664319515228
epoch: 40 loss: 0.3910042941570282
epoch: 60 loss: 0.3409908711910248
epoch: 80 loss: 0.2887084484100342
epoch: 100 loss: 0.25472864508628845
epoch: 120 loss: 0.22871072590351105
epoch: 140 loss: 0.20734436810016632
epoch: 160 loss: 0.18896348774433136
epoch: 180 loss: 0.173292875289917
epoch: 200 loss: 0.15965603291988373
epoch: 220 loss: 0.14779284596443176
epoch: 240 loss: 0.137494295835495
epoch: 260 loss: 0.12853200733661652
epoch: 280 loss: 0.12084188312292099
epoch: 300 loss: 0.11422470211982727
epoch: 320 loss: 0.1085757240653038
epoch: 340 loss: 0.10376542061567307
epoch: 360 loss: 0.09959365427494049
epoch: 380 loss: 0.09608905762434006

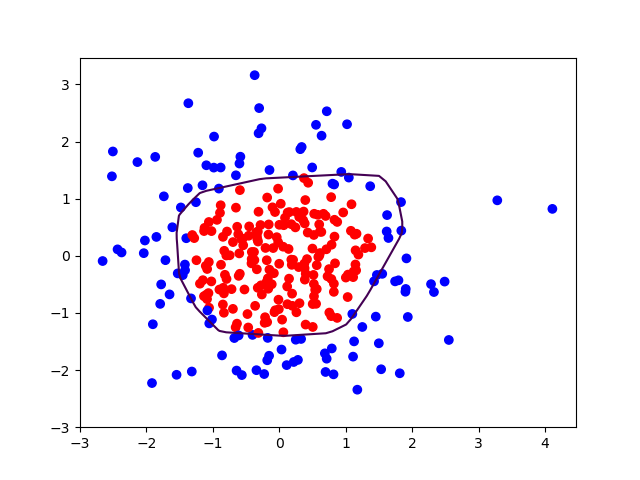
加入L2正则化后的曲线更平缓，有效缓解了过拟合。

优化器

优化算法可以分成一阶优化和二阶优化算法，其中一阶优化就是指的梯度算法及其变种，而二阶优化一般是用二阶导数（Hessian 矩阵）来计算，如牛顿法，由于需要计算Hessian阵和其逆矩阵，计算量较大，因此没有流行开来。这里主要总结一阶优化的各种梯度下降方法。

深度学习优化算法经历了SGD -> SGDM -> NAG ->AdaGrad -> AdaDelta -> Adam -> Nadam这样的发展历程。

当网络模型固定后，不同参数选取对模型的表达力影响很大。更新模型参数的过程，仿佛是教一个孩子认知世界，达到学龄的孩子，脑神经元的结构、规模是相似的，他们都具备了学习的潜力。但是不同的引导方法，会让孩子具备不同的能力，达到不同的高度。优化器就是引导神经网络更新参数的工具。

本节介绍五种常用的神经网络参数优化器。

定义：待优化参数w，损失函数loss，学习率lr，每次迭代一个batch，t表示当前batch迭代的总次数：

数据集中的数据是以batch为单位，批量喂入网络，每个batch通常包含$2^{n}$个数据，t表示当前batch迭代的总次数。

更新参数分四步完成：

  1. 计算t时刻损失函数关于当前参数的梯度：$ g{t} = \nabla loss = \frac{\partial loss}{\partial (w{t})} $

  2. 计算t时刻一阶动量 $ m{t} $ 和二阶动量 $ V{t} $

    一阶动量：与梯度相关的函数 $ m{t} = \phi(g{1}, g{2},…, g{t}) $

    二阶动量：与梯度平方相关的函数 $ V{t} = \psi(g{1}, g{2},…, g{t}) $

  3. 计算t时刻下降梯度： $ \eta{t} = lr·m{t} / \sqrt{V_{t}} $

  4. 计算t+1时刻参数：$ w{t+1} = w{t} - \eta{t} = w{t} - lr · m{t}/\sqrt{V{t}} $

对于步骤3、4对于各个算法都一样，主要区别在1、2上

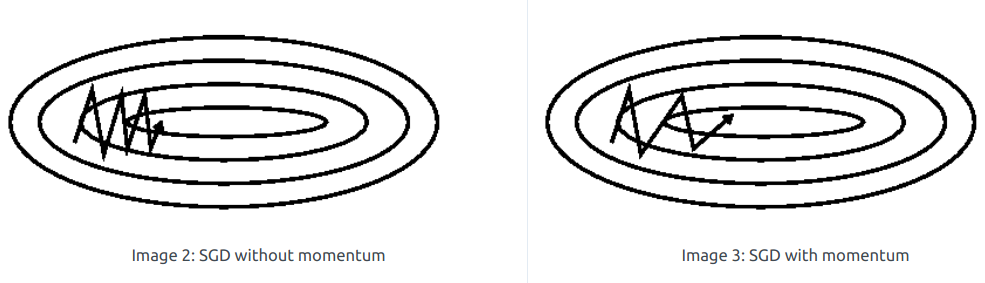
SGD随机梯度下降(无momentum)

没有动量的概念。

最大的缺点是下降速度慢，可能会在沟壑的两边持续震荡，停留在一个局部最优点。

$ m{t} = g{t} $

$ V_{t} = 1 $

$ \eta{t} = lr·m{t} / \sqrt{V{t}} = lr · g{t} $

对于单层网络的书写：

1
2
3
# sgd
w1.assign_sub(lr * grads[0])	#参数w1自更新
b1.assign_sub(lr * grads[1])	#参数b自更新

相较于p45_iris.py相比，只改动了四处

p32_sgd.py

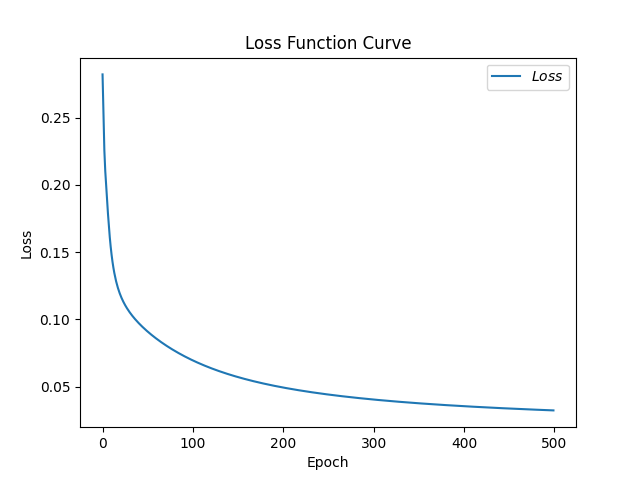
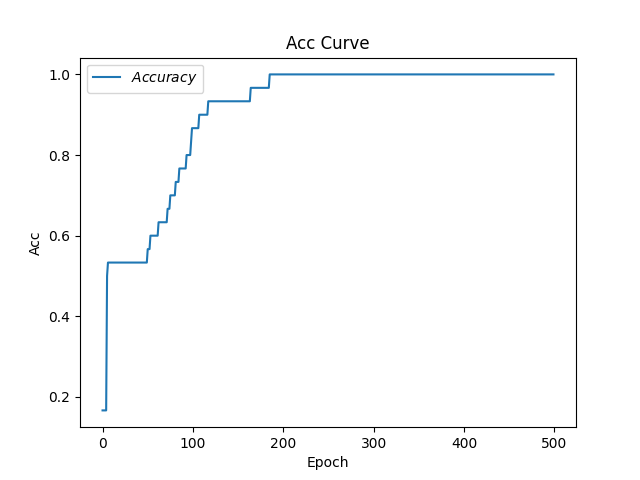
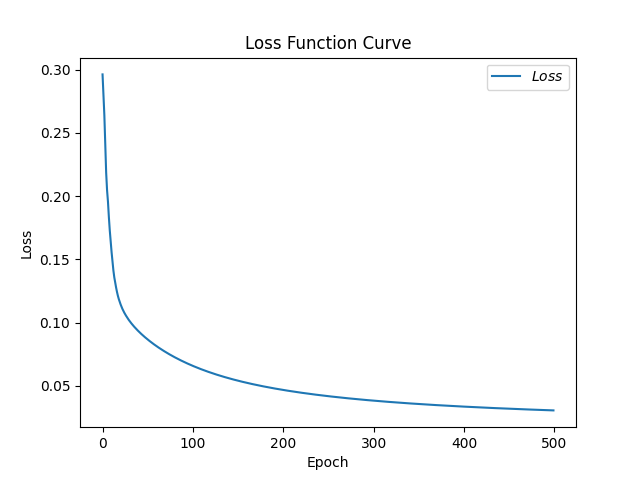
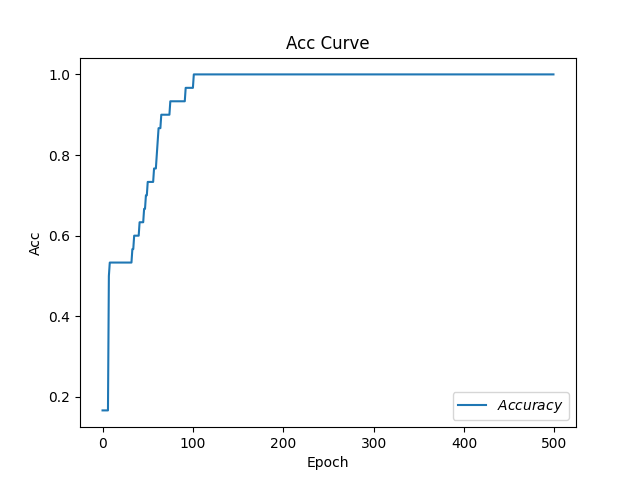
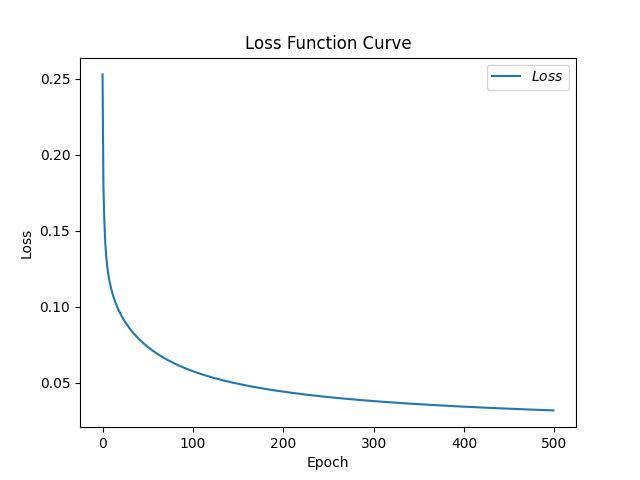
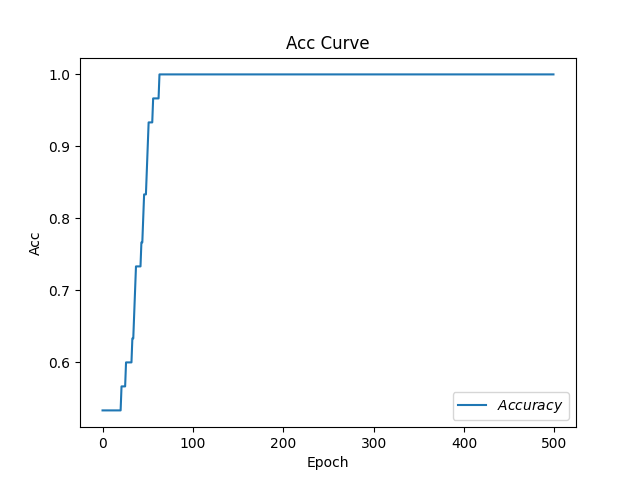
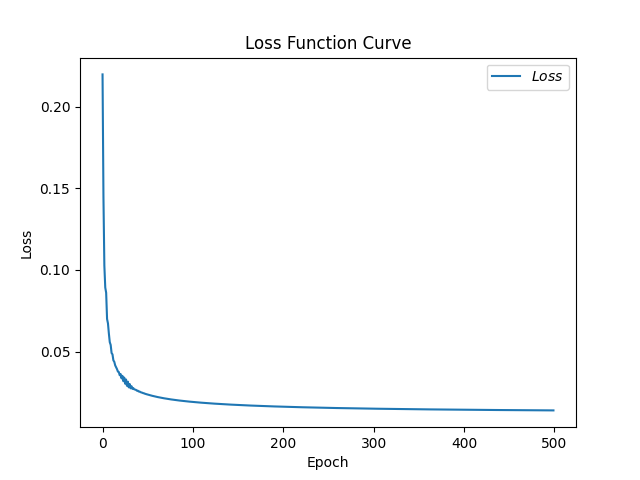
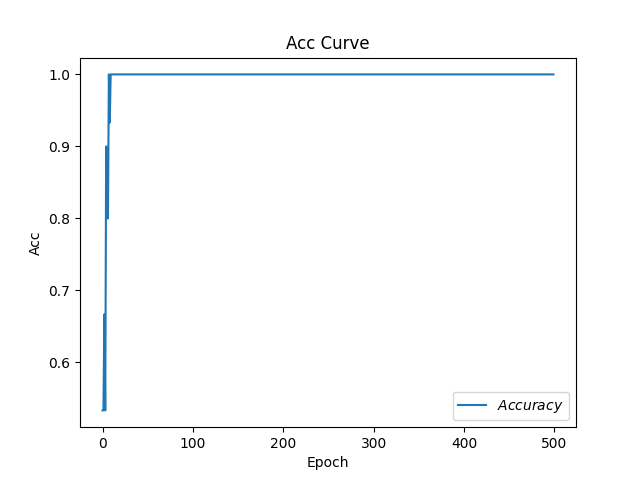
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
# 利用鸢尾花数据集，实现前向传播、反向传播，可视化loss曲线

# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
import time  ##1##

# 导入数据，分别为输入特征和标签
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target

# 随机打乱数据（因为原始数据是顺序的，顺序不打乱会影响准确率）
# seed: 随机数种子，是一个整数，当设置之后，每次生成的随机数都一样（为方便教学，以保每位同学结果一致）
np.random.seed(116)  # 使用相同的seed，保证输入特征和标签一一对应
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)

# 将打乱后的数据集分割为训练集和测试集，训练集为前120行，测试集为后30行
x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]

# 转换x的数据类型，否则后面矩阵相乘时会因数据类型不一致报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)

# from_tensor_slices函数使输入特征和标签值一一对应。（把数据集分批次，每个批次batch组数据）
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)

# 生成神经网络的参数，4个输入特征故，输入层为4个输入节点；因为3分类，故输出层为3个神经元
# 用tf.Variable()标记参数可训练
# 使用seed使每次生成的随机数相同（方便教学，使大家结果都一致，在现实使用时不写seed）
w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))

lr = 0.1  # 学习率为0.1
train_loss_results = []  # 将每轮的loss记录在此列表中，为后续画loss曲线提供数据
test_acc = []  # 将每轮的acc记录在此列表中，为后续画acc曲线提供数据
epoch = 500  # 循环500轮
loss_all = 0  # 每轮分4个step，loss_all记录四个step生成的4个loss的和

# 训练部分
now_time = time.time()  ##2##
for epoch in range(epoch):  # 数据集级别的循环，每个epoch循环一次数据集
    for step, (x_train, y_train) in enumerate(train_db):  # batch级别的循环 ，每个step循环一个batch
        with tf.GradientTape() as tape:  # with结构记录梯度信息
            y = tf.matmul(x_train, w1) + b1  # 神经网络乘加运算
            y = tf.nn.softmax(y)  # 使输出y符合概率分布（此操作后与独热码同量级，可相减求loss）
            y_ = tf.one_hot(y_train, depth=3)  # 将标签值转换为独热码格式，方便计算loss和accuracy
            loss = tf.reduce_mean(tf.square(y_ - y))  # 采用均方误差损失函数mse = mean(sum(y-out)^2)
            loss_all += loss.numpy()  # 将每个step计算出的loss累加，为后续求loss平均值提供数据，这样计算的loss更准确
        # 计算loss对各个参数的梯度
        grads = tape.gradient(loss, [w1, b1])

        # 实现梯度更新 w1 = w1 - lr * w1_grad    b = b - lr * b_grad
        w1.assign_sub(lr * grads[0])  # 参数w1自更新
        b1.assign_sub(lr * grads[1])  # 参数b自更新

    # 每个epoch，打印loss信息
    print("Epoch {}, loss: {}".format(epoch, loss_all / 4))
    train_loss_results.append(loss_all / 4)  # 将4个step的loss求平均记录在此变量中
    loss_all = 0  # loss_all归零，为记录下一个epoch的loss做准备

    # 测试部分
    # total_correct为预测对的样本个数, total_number为测试的总样本数，将这两个变量都初始化为0
    total_correct, total_number = 0, 0
    for x_test, y_test in test_db:
        # 使用更新后的参数进行预测
        y = tf.matmul(x_test, w1) + b1
        y = tf.nn.softmax(y)
        pred = tf.argmax(y, axis=1)  # 返回y中最大值的索引，即预测的分类
        # 将pred转换为y_test的数据类型
        pred = tf.cast(pred, dtype=y_test.dtype)
        # 若分类正确，则correct=1，否则为0，将bool型的结果转换为int型
        correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
        # 将每个batch的correct数加起来
        correct = tf.reduce_sum(correct)
        # 将所有batch中的correct数加起来
        total_correct += int(correct)
        # total_number为测试的总样本数，也就是x_test的行数，shape[0]返回变量的行数
        total_number += x_test.shape[0]
    # 总的准确率等于total_correct/total_number
    acc = total_correct / total_number
    test_acc.append(acc)
    print("Test_acc:", acc)
    print("--------------------------")
total_time = time.time() - now_time  ##3##
print("total_time", total_time)  ##4##

# 绘制 loss 曲线
plt.title('Loss Function Curve')  # 图片标题
plt.xlabel('Epoch')  # x轴变量名称
plt.ylabel('Loss')  # y轴变量名称
plt.plot(train_loss_results, label="$Loss$")  # 逐点画出trian_loss_results值并连线，连线图标是Loss
plt.legend()  # 画出曲线图标
plt.show()  # 画出图像

# 绘制 Accuracy 曲线
plt.title('Acc Curve')  # 图片标题
plt.xlabel('Epoch')  # x轴变量名称
plt.ylabel('Acc')  # y轴变量名称
plt.plot(test_acc, label="$Accuracy$")  # 逐点画出test_acc值并连线，连线图标是Accuracy
plt.legend()
plt.show()

# 本文件较 class1\p45_iris.py 仅添加四处时间记录  用 ##n## 标识
# 请将loss曲线、ACC曲线、total_time记录到 class2\优化器对比.docx  对比各优化器收敛情况
1
total_time 5.0308239459991455

pycharm导入包出现红线，使用conda命令行使用conda或者pip命令安装即可
如果红线消除但是运行提示DLL load failed: 找不到指定的程序。
在pycharm中设置运行环境增加PATH=C:\ProgramData\Anaconda3\Library\bin;

SGDM(含momentum的SGD)

动量法是一种使梯度向量向相关方向加速变化，抑制震荡，最终实现加速收敛的方法。
(Momentum is a method that helps accelerate SGD in the right direction and dampens oscillations. It adds a fraction of the update vector of the past time step to the current update vector. The momentum term increases for dimensions whose gradients point in the same directions and reduces updates for dimensions whose gradients change directions.)

为了抑制SGD的震荡，SGDM认为梯度下降过程可以加入惯性。下坡的时候，如果发现是陡坡，那就利用惯性跑的快一些。SGDM全称是SGD with Momentum，在SGD基础上引入了一阶动量：

一阶动量是各个时刻梯度方向的指数移动平均值，约等于最近 $ 1/(1-\beta{1}) $ 个时刻的梯度向量和的平均值。也就是说，t时刻的下降方向，不仅由当前点的梯度方向决定，而且由此前累积的下降方向决定。 $ \beta{1} $ 的经验值为0.9，这就意味着下降方向主要偏向此前累积的下降方向，并略微偏向当前时刻的下降方向。

在SGD基础上增加一阶动量。

$ m{t} $ 公式表示各时刻梯度方向的指数滑动平均值，和SGD相比，一阶动量的公式多了 $ m{t-1} $ 这一项， $ m_{t-1} $ 表示上一时刻的一阶动量，上一时刻的一阶动量占大头，$ \beta $ 是一个超参数，是个接近1的数值，经验值是0.9。

二阶动量在SGDM中仍是恒等于1的。

参数更新公式最重要的是把一阶动量和二阶动量计算出来

1
2
3
4
5
6
7
m_w, m_b = 0, 0
beta = 0.9
#sgd-momentun
m_w = beta * m_w + (1 - beta) * grads [0]
m_b = beta * m_b + (1 - beta) * grads [1]
w1.assign_sub(lr * m_w)
b1.assign_sub(lr * m_b)

p34_sgdm.py

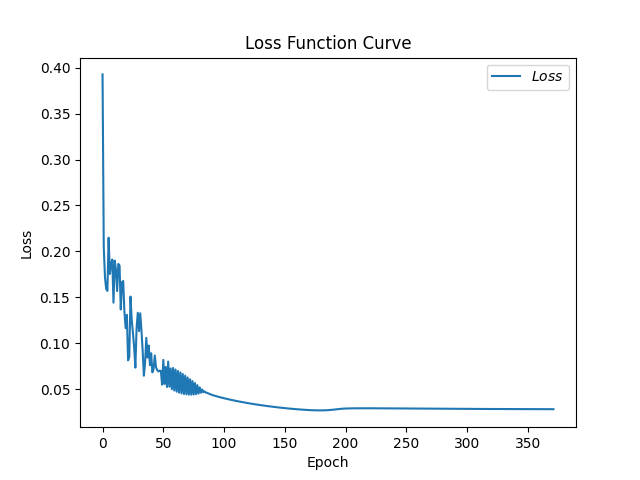
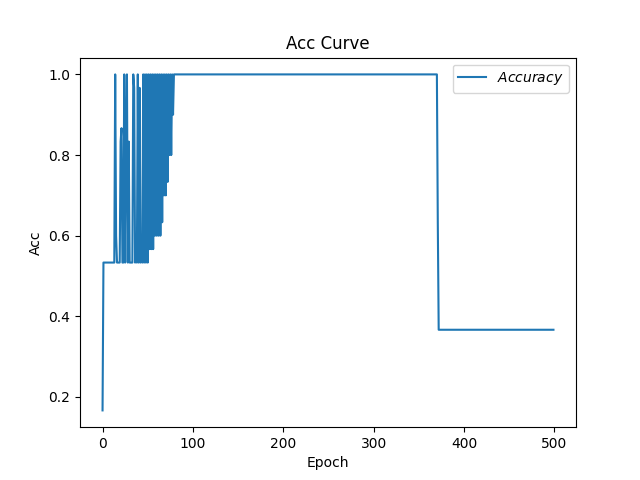
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
# 利用鸢尾花数据集，实现前向传播、反向传播，可视化loss曲线

# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
import time  ##1##

# 导入数据，分别为输入特征和标签
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target

# 随机打乱数据（因为原始数据是顺序的，顺序不打乱会影响准确率）
# seed: 随机数种子，是一个整数，当设置之后，每次生成的随机数都一样（为方便教学，以保每位同学结果一致）
np.random.seed(116)  # 使用相同的seed，保证输入特征和标签一一对应
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)

# 将打乱后的数据集分割为训练集和测试集，训练集为前120行，测试集为后30行
x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]

# 转换x的数据类型，否则后面矩阵相乘时会因数据类型不一致报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)

# from_tensor_slices函数使输入特征和标签值一一对应。（把数据集分批次，每个批次batch组数据）
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)

# 生成神经网络的参数，4个输入特征故，输入层为4个输入节点；因为3分类，故输出层为3个神经元
# 用tf.Variable()标记参数可训练
# 使用seed使每次生成的随机数相同（方便教学，使大家结果都一致，在现实使用时不写seed）
w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))

lr = 0.1  # 学习率为0.1
train_loss_results = []  # 将每轮的loss记录在此列表中，为后续画loss曲线提供数据
test_acc = []  # 将每轮的acc记录在此列表中，为后续画acc曲线提供数据
epoch = 500  # 循环500轮
loss_all = 0  # 每轮分4个step，loss_all记录四个step生成的4个loss的和

##########################################################################
m_w, m_b = 0, 0
beta = 0.9
##########################################################################

# 训练部分
now_time = time.time()  ##2##
for epoch in range(epoch):  # 数据集级别的循环，每个epoch循环一次数据集
    for step, (x_train, y_train) in enumerate(train_db):  # batch级别的循环 ，每个step循环一个batch
        with tf.GradientTape() as tape:  # with结构记录梯度信息
            y = tf.matmul(x_train, w1) + b1  # 神经网络乘加运算
            y = tf.nn.softmax(y)  # 使输出y符合概率分布（此操作后与独热码同量级，可相减求loss）
            y_ = tf.one_hot(y_train, depth=3)  # 将标签值转换为独热码格式，方便计算loss和accuracy
            loss = tf.reduce_mean(tf.square(y_ - y))  # 采用均方误差损失函数mse = mean(sum(y-out)^2)
            loss_all += loss.numpy()  # 将每个step计算出的loss累加，为后续求loss平均值提供数据，这样计算的loss更准确
        # 计算loss对各个参数的梯度
        grads = tape.gradient(loss, [w1, b1])

        ##########################################################################
        # sgd-momentun  
        m_w = beta * m_w + (1 - beta) * grads[0]
        m_b = beta * m_b + (1 - beta) * grads[1]
        w1.assign_sub(lr * m_w)
        b1.assign_sub(lr * m_b)
    ##########################################################################

    # 每个epoch，打印loss信息
    print("Epoch {}, loss: {}".format(epoch, loss_all / 4))
    train_loss_results.append(loss_all / 4)  # 将4个step的loss求平均记录在此变量中
    loss_all = 0  # loss_all归零，为记录下一个epoch的loss做准备

    # 测试部分
    # total_correct为预测对的样本个数, total_number为测试的总样本数，将这两个变量都初始化为0
    total_correct, total_number = 0, 0
    for x_test, y_test in test_db:
        # 使用更新后的参数进行预测
        y = tf.matmul(x_test, w1) + b1
        y = tf.nn.softmax(y)
        pred = tf.argmax(y, axis=1)  # 返回y中最大值的索引，即预测的分类
        # 将pred转换为y_test的数据类型
        pred = tf.cast(pred, dtype=y_test.dtype)
        # 若分类正确，则correct=1，否则为0，将bool型的结果转换为int型
        correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
        # 将每个batch的correct数加起来
        correct = tf.reduce_sum(correct)
        # 将所有batch中的correct数加起来
        total_correct += int(correct)
        # total_number为测试的总样本数，也就是x_test的行数，shape[0]返回变量的行数
        total_number += x_test.shape[0]
    # 总的准确率等于total_correct/total_number
    acc = total_correct / total_number
    test_acc.append(acc)
    print("Test_acc:", acc)
    print("--------------------------")
total_time = time.time() - now_time  ##3##
print("total_time", total_time)  ##4##

# 绘制 loss 曲线
plt.title('Loss Function Curve')  # 图片标题
plt.xlabel('Epoch')  # x轴变量名称
plt.ylabel('Loss')  # y轴变量名称
plt.plot(train_loss_results, label="$Loss$")  # 逐点画出trian_loss_results值并连线，连线图标是Loss
plt.legend()  # 画出曲线图标
plt.show()  # 画出图像

# 绘制 Accuracy 曲线
plt.title('Acc Curve')  # 图片标题
plt.xlabel('Epoch')  # x轴变量名称
plt.ylabel('Acc')  # y轴变量名称
plt.plot(test_acc, label="$Accuracy$")  # 逐点画出test_acc值并连线，连线图标是Accuracy
plt.legend()
plt.show()

# 请将loss曲线、ACC曲线、total_time记录到 class2\优化器对比.docx  对比各优化器收敛情况
1
total_time 5.486814260482788

SGD with Nesterov Acceleration

SGD 还有一个问题是会被困在一个局部最优点里。就像被一个小盆地周围的矮山挡住了视野，看不到更远的更深的沟壑。
NAG全称Nesterov Accelerated Gradient，是在SGD、SGDM的基础上的进一步改进，改进点在于步骤1。我们知道在时刻t的主要下降方向是由累积动量决定的，自己的梯度方向说了也不算，那与其看当前梯度方向，不如先看看如果跟着累积动量走了一步，那个时候再怎么走。因此，NAG在步骤1不计算当前位置的梯度方向，而是计算如果按照累积动量走了一步，考虑这个新地方的梯度方向。此时的梯度就变成了：

我们用这个梯度带入 SGDM 中计算 的式子里去，然后再计算当前时刻应有的梯度并更新这一次的参数。

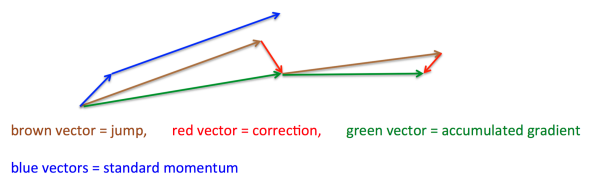
其基本思路如下图（转自Hinton的Lecture slides）：

首先，按照原来的更新方向更新一步（棕色线），然后计算该新位置的梯度方向（红色线），然后用这个梯度方向修正最终的更新方向（绿色线）。上图中描述了两步的更新示意图，其中蓝色线是标准momentum更新路径。

Adagrad

上述SGD算法一直存在一个超参数（Hyper-parameter），即学习率。超参数是训练前需要手动选择的参数，前缀”hyper”就是用于区别训练过程中可自动更新的参数。学习率可以理解为参数w沿着梯度g反方向变化的步长。

SGD对所有的参数使用统一的、固定的学习率，一个自然的想法是对每个参数设置不同的学习率，然而在大型网络中这是不切实际的。因此，为解决此问题，AdaGrad算法被提出，其做法是给学习率一个缩放比例，从而达到了自适应学习率的效果（Ada = Adaptive）。

其思想是：对于频繁更新的参数，不希望被单个样本影响太大，我们给它们很小的学习率；对于偶尔出现的参数，希望能多得到一些信息，我们给它较大的学习率。

那怎么样度量历史更新频率呢？为此引入二阶动量，即该维度上，所有梯度值的平方和：

回顾步骤 3 中的下降梯度：$ \eta{t} = \alpha · m{t} / \sqrt{V{t}} $ 可视为 $ \eta{t} = \frac{\alpha}{\sqrt{V{t}}} · m{t} $ ，即对学习率进行缩放。（一般为了防止分母为 0 ，会对二阶动量加一个平滑项，即$ \eta{t} = \alpha · m{t} / \sqrt{V_{t} + \varepsilon} $， $ \varepsilon $是一个非常小的数。）

AdaGrad 在稀疏数据场景下表现最好。因为对于频繁出现的参数，学习率衰减得快；对于稀疏的参数，学习率衰减得更慢。然而在实际很多情况下，二阶动量呈单调递增，累计从训练开始的梯度，学习率会很快减至0，导致参数不再更新，训练过程提前结束。

在SGD基础上增加二阶动量，可以对模型中的每个参数分配自适应学习率了。

Adagrad的一阶动量和SGD的一阶动量一样，是当前的梯度。

二阶动量是从现在开始，梯度平方的累计和。

$ m{t} = g{t} $

$ V{t} = \sum{\tau = 1}^{t} = g_{\tau}^{2} $

$ \eta{t} = lr·m{t} / \sqrt{V{t}} = lr · g{t} / (\sqrt{ \sum{\tau = 1}^{t} = g{\tau}^{2}}) $

一阶动量mt是当前时刻的梯度

二阶动量是梯度平方的累计和

$ m{t} = g{t} $

$ V{t} = \sum{\tau = 1}^{t} = g_{\tau}^{2} $

1
2
3
4
5
6
v_w, v_b = 0, 0
# adagrad
v_ w += tf.square(grads[0])
v_b += tf.square(grads[1])
W1.assign_sub(lr * grads[0] / tf.sqrt(v_w))
b1.assign_sub(lr * grads[1] / tf.sqrt(v_b))

p36_adagrad.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
# 利用鸢尾花数据集，实现前向传播、反向传播，可视化loss曲线

# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
import time  ##1##

# 导入数据，分别为输入特征和标签
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target

# 随机打乱数据（因为原始数据是顺序的，顺序不打乱会影响准确率）
# seed: 随机数种子，是一个整数，当设置之后，每次生成的随机数都一样（为方便教学，以保每位同学结果一致）
np.random.seed(116)  # 使用相同的seed，保证输入特征和标签一一对应
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)

# 将打乱后的数据集分割为训练集和测试集，训练集为前120行，测试集为后30行
x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]

# 转换x的数据类型，否则后面矩阵相乘时会因数据类型不一致报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)

# from_tensor_slices函数使输入特征和标签值一一对应。（把数据集分批次，每个批次batch组数据）
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)

# 生成神经网络的参数，4个输入特征故，输入层为4个输入节点；因为3分类，故输出层为3个神经元
# 用tf.Variable()标记参数可训练
# 使用seed使每次生成的随机数相同（方便教学，使大家结果都一致，在现实使用时不写seed）
w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))

lr = 0.1  # 学习率为0.1
train_loss_results = []  # 将每轮的loss记录在此列表中，为后续画loss曲线提供数据
test_acc = []  # 将每轮的acc记录在此列表中，为后续画acc曲线提供数据
epoch = 500  # 循环500轮
loss_all = 0  # 每轮分4个step，loss_all记录四个step生成的4个loss的和

##########################################################################
v_w, v_b = 0, 0
##########################################################################

# 训练部分
now_time = time.time()  ##2##
for epoch in range(epoch):  # 数据集级别的循环，每个epoch循环一次数据集
    for step, (x_train, y_train) in enumerate(train_db):  # batch级别的循环 ，每个step循环一个batch
        with tf.GradientTape() as tape:  # with结构记录梯度信息
            y = tf.matmul(x_train, w1) + b1  # 神经网络乘加运算
            y = tf.nn.softmax(y)  # 使输出y符合概率分布（此操作后与独热码同量级，可相减求loss）
            y_ = tf.one_hot(y_train, depth=3)  # 将标签值转换为独热码格式，方便计算loss和accuracy
            loss = tf.reduce_mean(tf.square(y_ - y))  # 采用均方误差损失函数mse = mean(sum(y-out)^2)
            loss_all += loss.numpy()  # 将每个step计算出的loss累加，为后续求loss平均值提供数据，这样计算的loss更准确
        # 计算loss对各个参数的梯度
        grads = tape.gradient(loss, [w1, b1])

        ##########################################################################
        # adagrad
        v_w += tf.square(grads[0])
        v_b += tf.square(grads[1])
        w1.assign_sub(lr * grads[0] / tf.sqrt(v_w))
        b1.assign_sub(lr * grads[1] / tf.sqrt(v_b))
    ##########################################################################

    # 每个epoch，打印loss信息
    print("Epoch {}, loss: {}".format(epoch, loss_all / 4))
    train_loss_results.append(loss_all / 4)  # 将4个step的loss求平均记录在此变量中
    loss_all = 0  # loss_all归零，为记录下一个epoch的loss做准备

    # 测试部分
    # total_correct为预测对的样本个数, total_number为测试的总样本数，将这两个变量都初始化为0
    total_correct, total_number = 0, 0
    for x_test, y_test in test_db:
        # 使用更新后的参数进行预测
        y = tf.matmul(x_test, w1) + b1
        y = tf.nn.softmax(y)
        pred = tf.argmax(y, axis=1)  # 返回y中最大值的索引，即预测的分类
        # 将pred转换为y_test的数据类型
        pred = tf.cast(pred, dtype=y_test.dtype)
        # 若分类正确，则correct=1，否则为0，将bool型的结果转换为int型
        correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
        # 将每个batch的correct数加起来
        correct = tf.reduce_sum(correct)
        # 将所有batch中的correct数加起来
        total_correct += int(correct)
        # total_number为测试的总样本数，也就是x_test的行数，shape[0]返回变量的行数
        total_number += x_test.shape[0]
    # 总的准确率等于total_correct/total_number
    acc = total_correct / total_number
    test_acc.append(acc)
    print("Test_acc:", acc)
    print("--------------------------")
total_time = time.time() - now_time  ##3##
print("total_time", total_time)  ##4##

# 绘制 loss 曲线
plt.title('Loss Function Curve')  # 图片标题
plt.xlabel('Epoch')  # x轴变量名称
plt.ylabel('Loss')  # y轴变量名称
plt.plot(train_loss_results, label="$Loss$")  # 逐点画出trian_loss_results值并连线，连线图标是Loss
plt.legend()  # 画出曲线图标
plt.show()  # 画出图像

# 绘制 Accuracy 曲线
plt.title('Acc Curve')  # 图片标题
plt.xlabel('Epoch')  # x轴变量名称
plt.ylabel('Acc')  # y轴变量名称
plt.plot(test_acc, label="$Accuracy$")  # 逐点画出test_acc值并连线，连线图标是Accuracy
plt.legend()
plt.show()

# 请将loss曲线、ACC曲线、total_time记录到 class2\优化器对比.docx  对比各优化器收敛情况
1
total_time 5.356388568878174

RMSProp

RMSProp算法的全称叫 Root Mean Square Prop，是由Geoffrey E. Hinton提出的一种优化算法（Hinton的课件见下图）。由于 AdaGrad 的学习率衰减太过激进，考虑改变二阶动量的计算策略：不累计全部梯度，只关注过去某一窗口内的梯度。修改的思路很直接，前面我们说过，指数移动平均值大约是过去一段时间的平均值，反映“局部的”参数信息，因此我们用这个方法来计算二阶累积动量：

在SGD基础上增加二阶动量

二阶动量v使用指数滑动平均值计算，表征的是过去一段时间的平均值

$ m{t} = g{t} $

$ V{t} = \beta · V{t-1} + (1 - \beta) · g_{t}^{2} $

$ \eta{t} = lr·m{t} / \sqrt{V{t}} = lr · g{t} / (\sqrt{\beta · V{t-1} + (1 - \beta) · g{t}^{2}}) $

1
2
3
4
5
6
7
v_w, v_b = 0, 0
beta = 0.9
# RMSProp
v_w = beta * v_w + (1 - beta) * tf.square(grads[0])
v_b = beta * v_b + (1 - beta) * tf.square(grads[1])
w1.assign_sub(lr * grads[0] / tf.sqrt(v_w))
bl.assign_sub(lr * grads[1] / tf.sqrt(v_b))

p38_rmsprop.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
# 利用鸢尾花数据集，实现前向传播、反向传播，可视化loss曲线

# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
import time  ##1##

# 导入数据，分别为输入特征和标签
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target

# 随机打乱数据（因为原始数据是顺序的，顺序不打乱会影响准确率）
# seed: 随机数种子，是一个整数，当设置之后，每次生成的随机数都一样（为方便教学，以保每位同学结果一致）
np.random.seed(116)  # 使用相同的seed，保证输入特征和标签一一对应
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)

# 将打乱后的数据集分割为训练集和测试集，训练集为前120行，测试集为后30行
x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]

# 转换x的数据类型，否则后面矩阵相乘时会因数据类型不一致报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)

# from_tensor_slices函数使输入特征和标签值一一对应。（把数据集分批次，每个批次batch组数据）
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)

# 生成神经网络的参数，4个输入特征故，输入层为4个输入节点；因为3分类，故输出层为3个神经元
# 用tf.Variable()标记参数可训练
# 使用seed使每次生成的随机数相同（方便教学，使大家结果都一致，在现实使用时不写seed）
w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))

lr = 0.1  # 学习率为0.1
train_loss_results = []  # 将每轮的loss记录在此列表中，为后续画loss曲线提供数据
test_acc = []  # 将每轮的acc记录在此列表中，为后续画acc曲线提供数据
epoch = 500  # 循环500轮
loss_all = 0  # 每轮分4个step，loss_all记录四个step生成的4个loss的和

##########################################################################
v_w, v_b = 0, 0
beta = 0.9
##########################################################################

# 训练部分
now_time = time.time()  ##2##
for epoch in range(epoch):  # 数据集级别的循环，每个epoch循环一次数据集
    for step, (x_train, y_train) in enumerate(train_db):  # batch级别的循环 ，每个step循环一个batch
        with tf.GradientTape() as tape:  # with结构记录梯度信息
            y = tf.matmul(x_train, w1) + b1  # 神经网络乘加运算
            y = tf.nn.softmax(y)  # 使输出y符合概率分布（此操作后与独热码同量级，可相减求loss）
            y_ = tf.one_hot(y_train, depth=3)  # 将标签值转换为独热码格式，方便计算loss和accuracy
            loss = tf.reduce_mean(tf.square(y_ - y))  # 采用均方误差损失函数mse = mean(sum(y-out)^2)
            loss_all += loss.numpy()  # 将每个step计算出的loss累加，为后续求loss平均值提供数据，这样计算的loss更准确
        # 计算loss对各个参数的梯度
        grads = tape.gradient(loss, [w1, b1])

        ##########################################################################
        # rmsprop
        v_w = beta * v_w + (1 - beta) * tf.square(grads[0])
        v_b = beta * v_b + (1 - beta) * tf.square(grads[1])
        w1.assign_sub(lr * grads[0] / tf.sqrt(v_w))
        b1.assign_sub(lr * grads[1] / tf.sqrt(v_b))
    ##########################################################################

    # 每个epoch，打印loss信息
    print("Epoch {}, loss: {}".format(epoch, loss_all / 4))
    train_loss_results.append(loss_all / 4)  # 将4个step的loss求平均记录在此变量中
    loss_all = 0  # loss_all归零，为记录下一个epoch的loss做准备

    # 测试部分
    # total_correct为预测对的样本个数, total_number为测试的总样本数，将这两个变量都初始化为0
    total_correct, total_number = 0, 0
    for x_test, y_test in test_db:
        # 使用更新后的参数进行预测
        y = tf.matmul(x_test, w1) + b1
        y = tf.nn.softmax(y)
        pred = tf.argmax(y, axis=1)  # 返回y中最大值的索引，即预测的分类
        # 将pred转换为y_test的数据类型
        pred = tf.cast(pred, dtype=y_test.dtype)
        # 若分类正确，则correct=1，否则为0，将bool型的结果转换为int型
        correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
        # 将每个batch的correct数加起来
        correct = tf.reduce_sum(correct)
        # 将所有batch中的correct数加起来
        total_correct += int(correct)
        # total_number为测试的总样本数，也就是x_test的行数，shape[0]返回变量的行数
        total_number += x_test.shape[0]
    # 总的准确率等于total_correct/total_number
    acc = total_correct / total_number
    test_acc.append(acc)
    print("Test_acc:", acc)
    print("--------------------------")
total_time = time.time() - now_time  ##3##
print("total_time", total_time)  ##4##

# 绘制 loss 曲线
plt.title('Loss Function Curve')  # 图片标题
plt.xlabel('Epoch')  # x轴变量名称
plt.ylabel('Loss')  # y轴变量名称
plt.plot(train_loss_results, label="$Loss$")  # 逐点画出trian_loss_results值并连线，连线图标是Loss
plt.legend()  # 画出曲线图标
plt.show()  # 画出图像

# 绘制 Accuracy 曲线
plt.title('Acc Curve')  # 图片标题
plt.xlabel('Epoch')  # x轴变量名称
plt.ylabel('Acc')  # y轴变量名称
plt.plot(test_acc, label="$Accuracy$")  # 逐点画出test_acc值并连线，连线图标是Accuracy
plt.legend()
plt.show()

# 请将loss曲线、ACC曲线、total_time记录到 class2\优化器对比.docx  对比各优化器收敛情况
1
total_time 5.9049718379974365

AdaDelta

为解决AdaGrad的学习率递减太快的问题，RMSProp和AdaDelta几乎同时独立被提出。

我们先看论文的AdaDelta算法，下图来自原论文：

对于上图算法的一点解释， $ RMS[g]{t} $ 是梯度$g$的均方根（Root Mean Square），
$ RMS[\Delta x]{t-1} $是$ \Delta x $的均方根：

我们可以看到AdaDelta与RMSprop仅仅是分子项不同，为了与前面公式保持一致，在此用$\sqrt{U_{t}}$表示$\eta$的均方根：

我们可以看到AdaDelta与RMSprop仅仅是分子项不同，为了与前面公式保持一致，在此用
表示 的均方根：

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
# AdaDelta
beta = 0.999
v_w = beta * v_w + (1 - beta) * tf.square(grads[0])
v_b = beta * v_b + (1 - beta) * tf.square(grads[1])

delta_w = tf.sqrt(u_w) * grads[0] / tf.sqrt(v_w)
delta_b = tf.sqrt(u_b) * grads[1] / tf.sqrt(v_b)

u_w = beta * u_w + (1 - beta) * tf.square(delta_w)
u_b = beta * u_b + (1 - beta) * tf.square(delta_b)

w1.assign_sub(delta_w)
b1.assign_sub(delta_b)

Adam

Adam名字来源是adaptive moment estimation。Our method is designed to combine the advantages of two recently popular methods: AdaGrad (Duchi et al., 2011), which works well with sparse gradients, and RMSProp (Tieleman & Hinton, 2012), which works well in on-line and non-stationary settings。也就是说，adam融合了Adagrad和RMSprop的思想。

谈到这里，Adam的出现就很自然而然了——它们是前述方法的集大成者。我们看到，SGDM在SGD基础上增加了一阶动量，AdaGrad、RMSProp和AdaDelta在SGD基础上增加了二阶动量。把一阶动量和二阶动量结合起来，再修正偏差，就是Adam了。

同时引入了SGDM一阶动量和RMSProp二阶动量，并在此基础上增加了两个修正项，把修正后的一阶动量和二阶动量带入参数更新公式。

SGDM一阶动量：

RMSProp二阶动量：

其中，参数经验值是$ \beta{1} = 0.9 $ 和 $ \beta{2} = 0.999 $

一阶动量和二阶动量都是按照指数移动平均值进行计算的。初始化 $ m{0} = 0, V{0} = 0 $ ，在初期，迭代得到的 $ m{t} $ 和 $ V{t} $ 会接近于0。我们可以通过对 $ m{t} $ 和 $ V{t} $ 进行偏差修正来解决这一问题：

修正一阶动量的偏差：$ \widehat{m{t}} = \frac{m{t}}{1 - \beta_{1}^{t}} $

修正二阶动量的偏差：$ \widehat{V{t}} = \frac{V{t}}{1 - \beta_{2}^{t}} $

adam一阶动量是和含momentum的SGD一阶动量一样

二阶动量表达是和RMSProp的二阶动量表达式一样

$ \widehat{m{t}} = \frac{m{t}}{1 - \beta_{1}^{t}} $

$ \widehat{V{t}} = \frac{V{t}}{1 - \beta_{2}^{t}} $

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
m_w, m_b = 0, 0
v_w, v_b = 0, 0
beta1, beta2 = 0.9, 0.999
delta_w, delta_b = 0, 0
global_step = 0

#adam
m_w = beta1 * m_w + (1 - beta1) * grads[0]
m_b = beta1 * m_b + (1 - beta1) * grads[1]
v_w = beta2 * v_w + (1 - beta2) * tf.square(grads[0])
v_b = beta2 * v_b + (1 - beta2) * tf.square(grads[1])

#global_step是从训练开始到当前时所经历的总batch数
m_w_correction = m_w / (1 - tf.pow(beta1, int(global_step)))
m_b_correction = m_b / (1 - tf.pow(beta1, int(global_step)))
v_w_correction = v_w / (1 - tf.pow(beta2, int(global_step)))
v_b_correction = v_b / (1 - tf.pow(beta2, int(global_step)))

w1.assign_sub(lr * m_w_correction / tf.sqrt(v_w_correction))
b1.assign_sub(lr * m_b_correction / tf.sqrt(v_b_correction))

p40_adam.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
# 利用鸢尾花数据集，实现前向传播、反向传播，可视化loss曲线

# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
import time  ##1##

# 导入数据，分别为输入特征和标签
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target

# 随机打乱数据（因为原始数据是顺序的，顺序不打乱会影响准确率）
# seed: 随机数种子，是一个整数，当设置之后，每次生成的随机数都一样（为方便教学，以保每位同学结果一致）
np.random.seed(116)  # 使用相同的seed，保证输入特征和标签一一对应
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)

# 将打乱后的数据集分割为训练集和测试集，训练集为前120行，测试集为后30行
x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]

# 转换x的数据类型，否则后面矩阵相乘时会因数据类型不一致报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)

# from_tensor_slices函数使输入特征和标签值一一对应。（把数据集分批次，每个批次batch组数据）
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)

# 生成神经网络的参数，4个输入特征故，输入层为4个输入节点；因为3分类，故输出层为3个神经元
# 用tf.Variable()标记参数可训练
# 使用seed使每次生成的随机数相同（方便教学，使大家结果都一致，在现实使用时不写seed）
w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))

lr = 0.1  # 学习率为0.1
train_loss_results = []  # 将每轮的loss记录在此列表中，为后续画loss曲线提供数据
test_acc = []  # 将每轮的acc记录在此列表中，为后续画acc曲线提供数据
epoch = 500  # 循环500轮
loss_all = 0  # 每轮分4个step，loss_all记录四个step生成的4个loss的和

##########################################################################
m_w, m_b = 0, 0
v_w, v_b = 0, 0
beta1, beta2 = 0.9, 0.999
delta_w, delta_b = 0, 0
global_step = 0
##########################################################################

# 训练部分
now_time = time.time()  ##2##
for epoch in range(epoch):  # 数据集级别的循环，每个epoch循环一次数据集
    for step, (x_train, y_train) in enumerate(train_db):  # batch级别的循环 ，每个step循环一个batch
 ##########################################################################       
        global_step += 1
 ##########################################################################       
        with tf.GradientTape() as tape:  # with结构记录梯度信息
            y = tf.matmul(x_train, w1) + b1  # 神经网络乘加运算
            y = tf.nn.softmax(y)  # 使输出y符合概率分布（此操作后与独热码同量级，可相减求loss）
            y_ = tf.one_hot(y_train, depth=3)  # 将标签值转换为独热码格式，方便计算loss和accuracy
            loss = tf.reduce_mean(tf.square(y_ - y))  # 采用均方误差损失函数mse = mean(sum(y-out)^2)
            loss_all += loss.numpy()  # 将每个step计算出的loss累加，为后续求loss平均值提供数据，这样计算的loss更准确
        # 计算loss对各个参数的梯度
        grads = tape.gradient(loss, [w1, b1])

##########################################################################
 # adam
        m_w = beta1 * m_w + (1 - beta1) * grads[0]
        m_b = beta1 * m_b + (1 - beta1) * grads[1]
        v_w = beta2 * v_w + (1 - beta2) * tf.square(grads[0])
        v_b = beta2 * v_b + (1 - beta2) * tf.square(grads[1])

        m_w_correction = m_w / (1 - tf.pow(beta1, int(global_step)))
        m_b_correction = m_b / (1 - tf.pow(beta1, int(global_step)))
        v_w_correction = v_w / (1 - tf.pow(beta2, int(global_step)))
        v_b_correction = v_b / (1 - tf.pow(beta2, int(global_step)))

        w1.assign_sub(lr * m_w_correction / tf.sqrt(v_w_correction))
        b1.assign_sub(lr * m_b_correction / tf.sqrt(v_b_correction))
##########################################################################

    # 每个epoch，打印loss信息
    print("Epoch {}, loss: {}".format(epoch, loss_all / 4))
    train_loss_results.append(loss_all / 4)  # 将4个step的loss求平均记录在此变量中
    loss_all = 0  # loss_all归零，为记录下一个epoch的loss做准备

    # 测试部分
    # total_correct为预测对的样本个数, total_number为测试的总样本数，将这两个变量都初始化为0
    total_correct, total_number = 0, 0
    for x_test, y_test in test_db:
        # 使用更新后的参数进行预测
        y = tf.matmul(x_test, w1) + b1
        y = tf.nn.softmax(y)
        pred = tf.argmax(y, axis=1)  # 返回y中最大值的索引，即预测的分类
        # 将pred转换为y_test的数据类型
        pred = tf.cast(pred, dtype=y_test.dtype)
        # 若分类正确，则correct=1，否则为0，将bool型的结果转换为int型
        correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
        # 将每个batch的correct数加起来
        correct = tf.reduce_sum(correct)
        # 将所有batch中的correct数加起来
        total_correct += int(correct)
        # total_number为测试的总样本数，也就是x_test的行数，shape[0]返回变量的行数
        total_number += x_test.shape[0]
    # 总的准确率等于total_correct/total_number
    acc = total_correct / total_number
    test_acc.append(acc)
    print("Test_acc:", acc)
    print("--------------------------")
total_time = time.time() - now_time  ##3##
print("total_time", total_time)  ##4##

# 绘制 loss 曲线
plt.title('Loss Function Curve')  # 图片标题
plt.xlabel('Epoch')  # x轴变量名称
plt.ylabel('Loss')  # y轴变量名称
plt.plot(train_loss_results, label="$Loss$")  # 逐点画出trian_loss_results值并连线，连线图标是Loss
plt.legend()  # 画出曲线图标
plt.show()  # 画出图像

# 绘制 Accuracy 曲线
plt.title('Acc Curve')  # 图片标题
plt.xlabel('Epoch')  # x轴变量名称
plt.ylabel('Acc')  # y轴变量名称
plt.plot(test_acc, label="$Accuracy$")  # 逐点画出test_acc值并连线，连线图标是Accuracy
plt.legend()
plt.show()

# 请将loss曲线、ACC曲线、total_time记录到 class2\优化器对比.docx  对比各优化器收敛情况
1
total_time 6.299233913421631

五种优化器对比总结

各种优化器来源

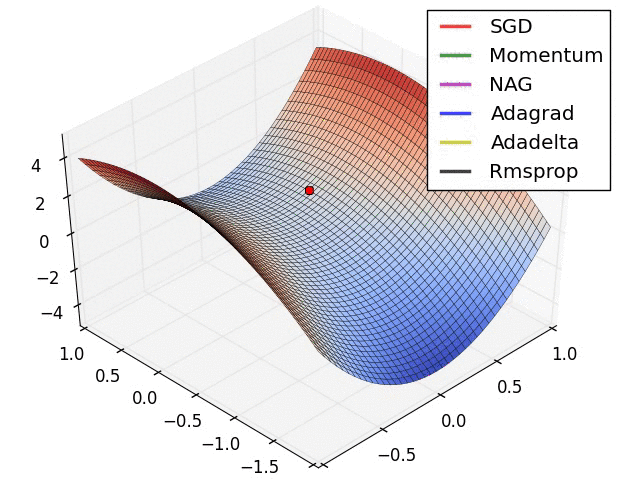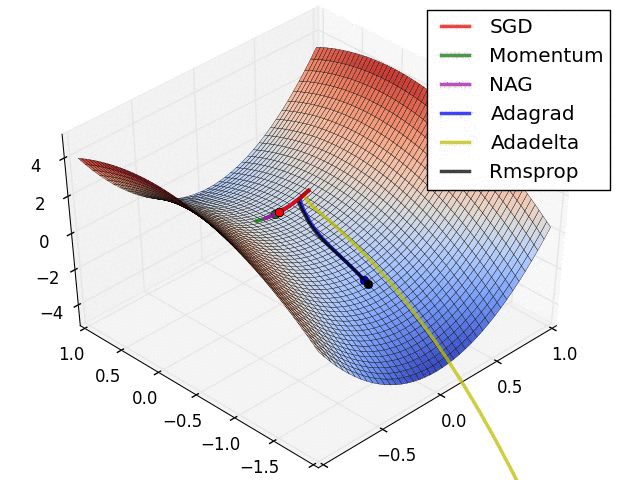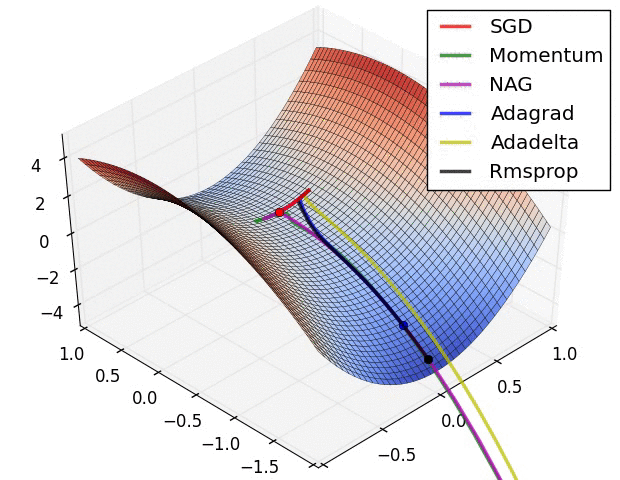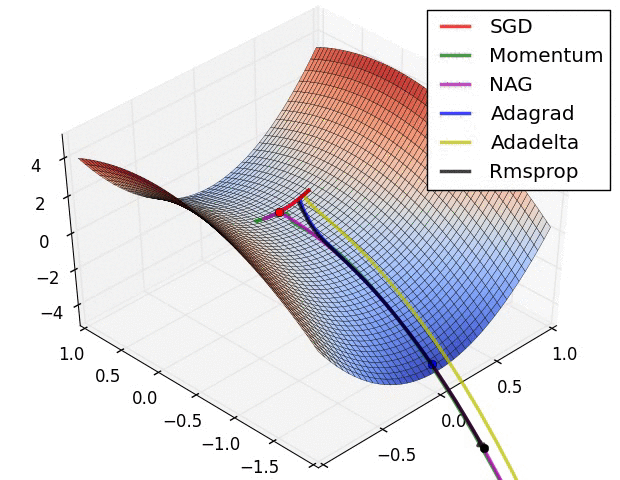
Visualizing Optimization Algos

Algos without scaling based on gradient information really struggle to break symmetry here - SGD gets no where and Nesterov Accelerated Gradient / Momentum exhibits oscillations until they build up velocity in the optimization direction.
没有基于梯度信息进行缩放的算法在这里真的很难打破对称性——SGD没有位置，Nesterov加速梯度/动量表现出振荡，直到它们在优化方向上建立速度。

Algos that scale step size based on the gradient quickly break symmetry and begin descent.
基于梯度缩放步长的算法会迅速打破对称性并开始下降。

Due to the large initial gradient, velocity based techniques shoot off and bounce around - adagrad almost goes unstable for the same reason.
由于初始梯度大，基于速度的技术在阿达格勒附近发射和反弹几乎会因为同样的原因而变得不稳定。

Algos that scale gradients/step sizes like adadelta and RMSProp proceed more like accelerated SGD and handle large gradients with more stability.
像adadelta和RMSProp这样缩放梯度/步长的算法更像加速SGD，并且更稳定地处理大梯度。

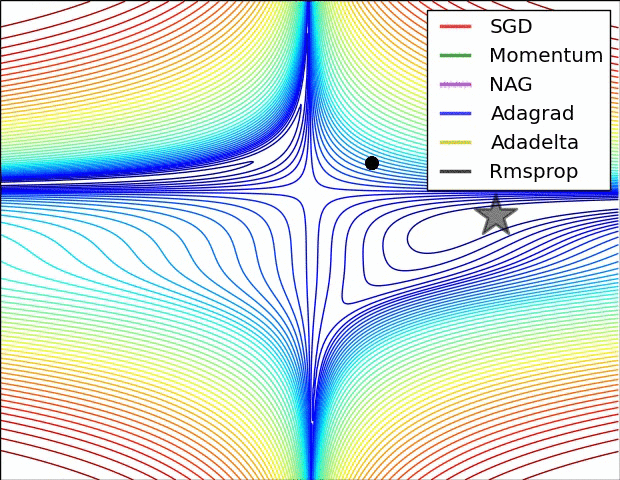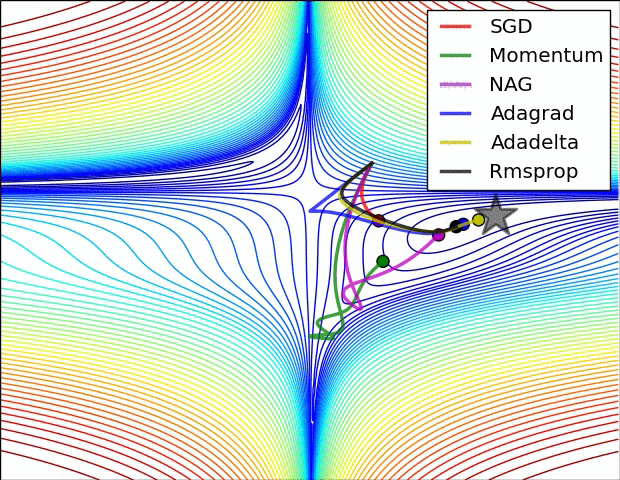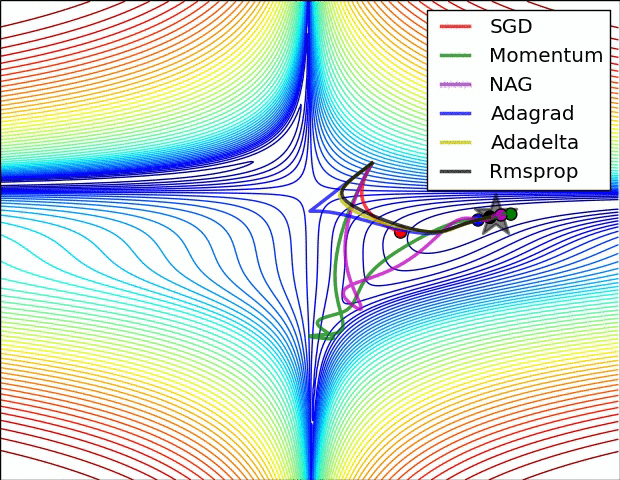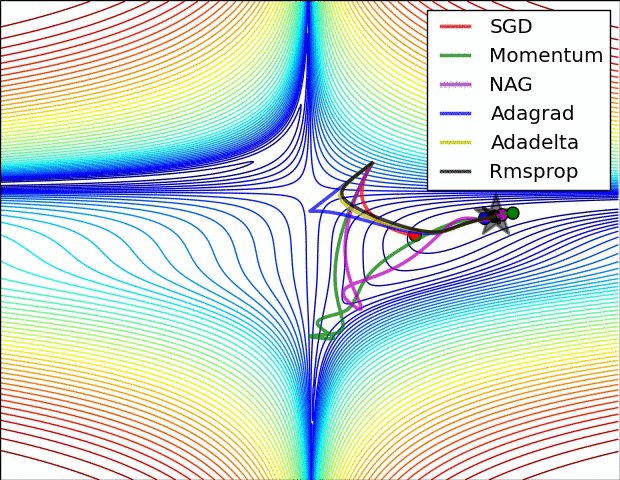
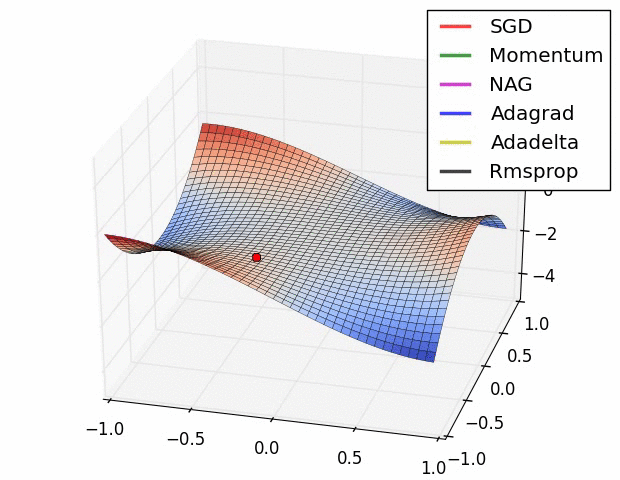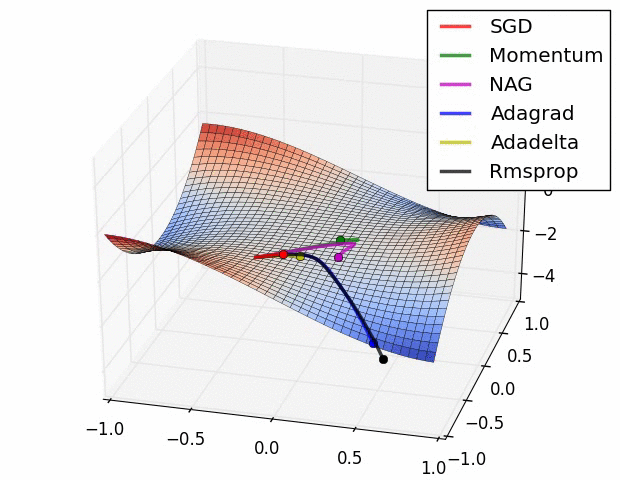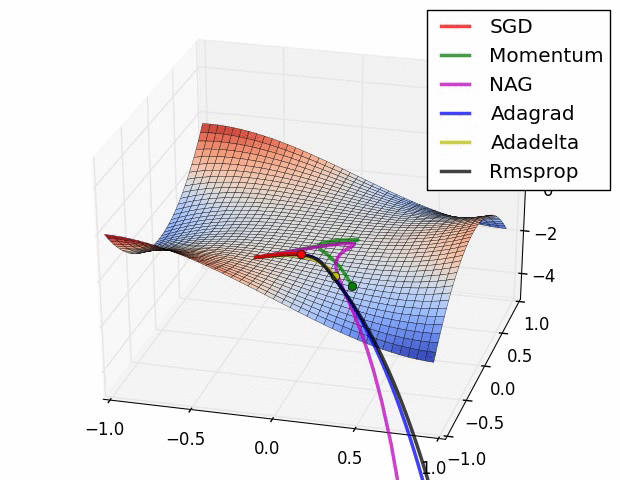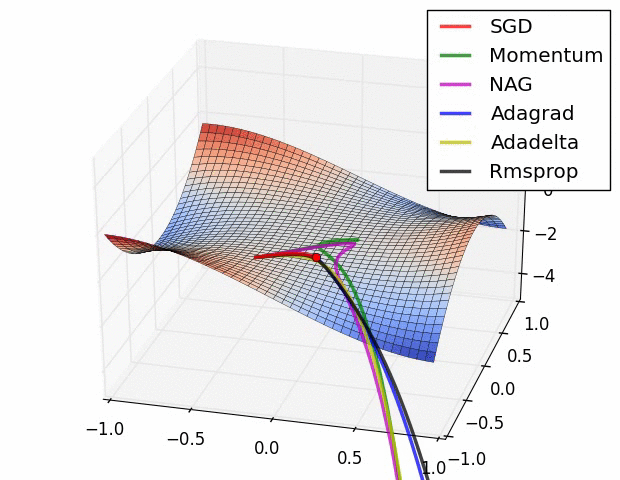
Behavior around a saddle point.
鞍点周围的行为。

NAG/Momentum again like to explore around, almost taking a different path.
NAG/Momentum再次喜欢四处探索，几乎走上了一条不同的道路。

Adadelta/Adagrad/RMSProp proceed like accelerated SGD.
阿达德尔塔/阿达格拉德/RMSProp像加速SGD一样进行。

SGD

参数更新公式最重要的是把一阶动量和二阶动量计算出来

1
total_time 5.486814260482788

SGDM

参数更新公式最重要的是把一阶动量和二阶动量计算出来

1
total_time 5.486814260482788

Adagrad

$ m{t} = g{t} $

$ V{t} = \sum{\tau = 1}^{t} = g_{\tau}^{2} $

$ \eta{t} = lr·m{t} / \sqrt{V{t}} = lr · g{t} / (\sqrt{ \sum{\tau = 1}^{t} = g{\tau}^{2}}) $

一阶动量mt是当前时刻的梯度

二阶动量是梯度平方的累计和

$ m{t} = g{t} $

$ V{t} = \sum{\tau = 1}^{t} = g_{\tau}^{2} $

1
total_time 5.356388568878174

RMSProp

$ m{t} = g{t} $

$ V{t} = \beta · V{t-1} + (1 - \beta) · g_{t}^{2} $

$ \eta{t} = lr·m{t} / \sqrt{V{t}} = lr · g{t} / (\sqrt{\beta · V{t-1} + (1 - \beta) · g{t}^{2}}) $

$ m{t} = g{t} $

$ V{t} = \beta · V{t-1} + (1 - \beta) · g_{t}^{2} $

1
total_time 5.9049718379974365

Adam

修正一阶动量的偏差：$ \widehat{m{t}} = \frac{m{t}}{1 - \beta_{1}^{t}} $

修正二阶动量的偏差：$ \widehat{V{t}} = \frac{V{t}}{1 - \beta_{2}^{t}} $

adam一阶动量是和含momentum的SGD一阶动量一样

二阶动量表达是和RMSProp的二阶动量表达式一样

$ \widehat{m{t}} = \frac{m{t}}{1 - \beta_{1}^{t}} $

$ \widehat{V{t}} = \frac{V{t}}{1 - \beta_{2}^{t}} $

1
total_time 6.299233913421631

其他API

tf.cast

1
2
3
tf.cast(
	x, dtype, name=None
)
  • 功能：转换数据（张量）类型。
  • 参数：
    x：待转换的数据（张量）
    dtype：目标数据类型
    name：定义操作的名称（可选参数）
  • 返回：数据类型为dtype，shape与x相同的张量
  • 例子：
    1
    2
    3
    x = tf.constant([1.8, 2.2], dtype=tf.float32)
    print(tf.cast(x, tf.int32))
    >>> tf.Tensor([1 2], shape=(2,), dtype=int32)

tf.random.normal

1
2
3
tf.random.normal(
	shape, mean=0.0, stddev=1.0, dtype=tf.dtypes.float32, seed=None, name=None
)
  • 功能：生成服从正态分布的随机值
  • 参数：
    x：一维张量
    mean：正态分布的均值
    stddev：正态分布的方差
  • 返回：满足指定shape并且服从正态分布的张量
  • 例子：
    1
    2
    3
    4
    5
    6
    tf.random.normal([3, 5])
    >>> <tf.Tensor: id=7, shape=(3, 5), dtype=float32, numpy=
    array([[-0.3951666 , -0.06858674, 0.29626969, 0.8070933 , -0.81376624],
    [ 0.09532423, -0.20840745, 0.37404788, 0.5459829 , 0.17986278],
    [-1.0439969 , -0.8826001 , 0.7081867 , -0.40955627, -2.6596873 ]],
    dtype=float32)>

tf.where

1
2
3
tf.where(
	condition, x=None, y=None, name=None
)
  • 功能：根据condition，取x或y中的值。如果为True，对应位置取x的值；如果为False，对应位置取y的值。
  • 参数：
    condition：bool型张量
    x：与y shape相同的张量
    y：与x shape相同的张量
  • 返回：shape与x相同的张量
  • 例子：
1
2
print(tf.where([True, False, True, False], [1,2,3,4], [5,6,7,8]))
>>> tf.Tensor([1 6 3 8], shape=(4,), dtype=int32)
文章作者: HibisciDai
文章链接: http://hibiscidai.com/2023/02/16/人工智能实践-Tensorflow笔记-MOOC-第二讲神经网络优化/
版权声明: 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 HibisciDai！
学习笔记TensorflowTensorflowMOOC
好用、实惠、稳定的梯子,点击这里